Question

【题目】综合与实践：

问题情境：

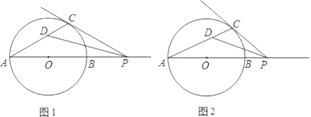
如图 1，AB∥CD，∠PAB=25°，∠PCD=37°，求∠APC的度数，小明的思路是：过点P作PE∥AB，通过平行线性质来求∠APC

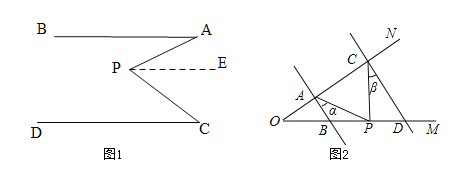
问题解决：

（1）按小明的思路，易求得∠APC 的度数为 °；

问题迁移：

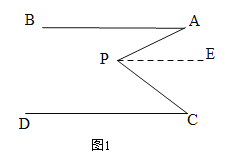
如图 2，AB∥CD，点 P 在射线 OM 上运动，记∠PAB=α，∠PCD=β．

（2）当点 P 在 B，D 两点之间运动时，问∠APC 与α，β 之间有何数量关系？ 请说明理由；

拓展延伸：

（3）在（2）的条件下，如果点 P 在 B，D 两点外侧运动时 （点 P 与点 O，B，D 三点不重合）请你直接写出当点 P 在线段 OB 上时，∠APC 与 α，β 之间的数量关系 ，点 P 在射线 DM 上时，∠APC 与 α，β 之间的数量关系 ．

Answer 1

【答案】（1）62；（2），理由详见解析；（3）；．

【解析】

（1）根据平行线的性质，得到∠APE=∠PAB=25°，∠CPE=∠PCD=37°，即可得到∠APC；

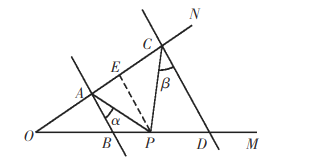
（2）过P作PE∥AD交AC于E，推出AB∥PE∥DC，根据平行线的性质得出∠APE=α，∠CPE=β，即可得出答案；

（3）分两种情况：P在BD延长线上；P在DB延长线上，分别画出图形，根据平行线的性质得出∠α=∠APE，∠β=∠CPE，即可得出答案；

解：如图1，过P作PE∥AB，

∵AB∥CD，

∴PE∥AB∥CD，

∴∠APE=∠PAB=25°，∠CPE=∠PCD=37°，

∴∠APC=25°+37°=62°；

故答案为：；

与之间的数量关系是：；

理由：如图，过点作交于点，

∵，

；

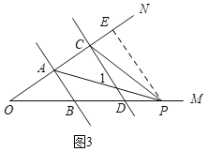
如图3，所示，当P在射线上时，

过P作PE∥AB，交AC于E，

∵AB∥CD，

∴AB∥PE∥CD，

∴∠1=∠PAB=α，

∵∠1=∠APC+∠PCD，

∴∠APC=∠1∠PCD，

∴∠APC=αβ，

∴当P在射线上时，；

如图4所示，当P在线段OB上时，

同理可得：∠APC=βα，

∴当P在线段OB上时，．

故答案为：；.