Question

【题目】如图：正方形OABC置于坐标系中，B的坐标是（-4，4），点D是边OA上一动点，以OD为边在第一象限内作正方形ODEF．

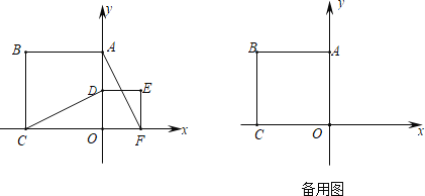
（1）CD与AF有怎样的位置关系，猜想并证明；

（2）当OD=______时，直线CD平分线段AF；

（3）在OD=2时，将正方形ODEF绕点O逆时针旋转α°（0°＜α°＜180°），求当C、D、E共线时D的坐标．

Answer 1

【答案】（1）CD⊥AF，理由见解析；（2）4-4；（3）（-1，）或（-1，-）．

【解析】

（1）证明△COD△AOF，可得∠OCD=∠OAF，根据三角形的内角和定理可得：∠AGD=∠DOC=90°，从而得结论；

（2）如图2，根据线段垂直平分线的性质得：AC=CF，列方程可得结论；

（3）分两种情况：①如图3，当D在第二象限时，过D作DG⊥x轴于G，根据直角三角形30度角的性质可得DG和OG的长，由此得D的坐标；

②如图4，当D在第三象限时，同理可得结论．

解：（1）CD⊥AF，理由是：

如图1，延长CD交AF于G，

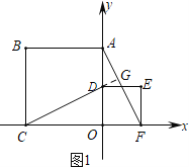
∵四边形OABC和ODEF是正方形，

∴AO=OC，∠COD=∠AOF=90°，OF=OD，

∴△COD△AOF（SAS），

∴∠OCD=∠OAF，

∵∠ADG=∠CDO，

∴∠AGD=∠DOC=90°，

∴CD⊥AF；

（2）设OD=x，连接AC，如图2，

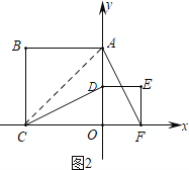
当直线CD平分线段AF时，AC=CF，

∵B的坐标是（-4，4），

∴AC=4，

∴4=4+x，

x=4-4，

则当OD=4-4时，直线CD平分线段AF；

故答案为：4-4；

（3）分两种情况：

①如图3，当D在第二象限时，过D作DG⊥x轴于G，

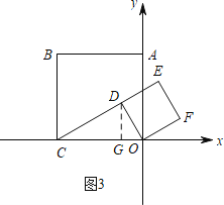
∵C、D、E共线，

∴∠CDO=∠ODE=90°，

Rt△ODC中，OD=2，OC=4，

∴∠OCD=30°，CD=2，

∴DG=CD=，CG=3，

∴OG=4-3=1，

∴D（-1，），

②如图4，当D在第三象限时，过D作DG⊥x轴于G，

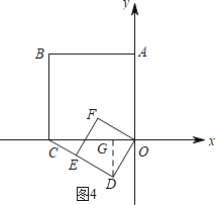
同理得：OG=1，DG=，

∴D（-1，-），

综上，点D的坐标为：（-1，）或（-1，-）．