Question

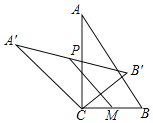
【题目】已知，如图，在中，，于，的平分线交于，交于，的角平分线交于，交于．

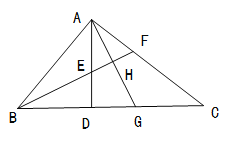
（1）求证:；

（2）判断与的位置关系，并说明理由．

（3）再找出二组相等的线段：①________；②___________．

Answer 1

【答案】（1）见解析；（2），理由见解析；（3）①，②

【解析】

(1)利用等角的余角相等结合对顶角相等即可证明结论；

(2)利用(1)的结论，根据等腰三角形三线合一的性质即可证得与相互垂直；

(3)根据(2)的结论知，利用三角形外角的性质可得∠AGB=∠GAC+∠C，利用同角的余角相等的性质证得∠BAD=∠C，根据角平分线的性质即可证得∠AGB=∠BAG，得到BA=BG．

(1) ∵，，

∴，，

又∵平分，

∴，

∴，

∵，

∴，

∴；

(2)，

理由如下：

由(1)得，

∵平分，

∴(三线合一)，

∴；

(3)由(2)得：；

∵，，

∴，，

∴，

∵平分，

∴，

∵∠AGB=∠GAC+∠C，∠BAG=∠BAD+∠DAG，

∴∠AGB=∠BAG，

∴．

故答案为：，．