题目内容
如图,在平面直角坐标系中,顶点为(3,4)的抛物线交 y轴与A点,交x轴与B、C两点(点B在点C的左侧),已知A点坐标为(0,-5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线与点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并给出证明.
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形.若存在,求点P的坐标;若不存在,请说明理由.
解:(1)∵抛物线的顶点为(3,4),∴可设此抛物线的解析式为: 。
。
∵此抛物线过点A(0,-5),∴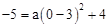 ,解得
,解得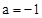 。
。
∴此抛物线的解析式为: ,即
,即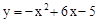 。
。
(2)此时抛物线的对称轴与⊙C相离。证明如下:
令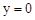 ,即
,即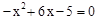 ,得x=1或x=5,
,得x=1或x=5,
∴B(1,0),C(5,0)。
令x=1,得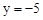 ,∴A(0,-5)。
,∴A(0,-5)。
如图,过点C作CE⊥BD于点E,作抛物线的对称轴交x轴于点F,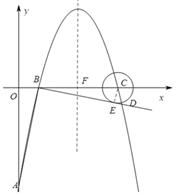
∵AB⊥BD,∴∠ABO=900-∠ABO=∠CBE。
∵∠AOB=∠BEC=900,∴△AOB∽△BEC。
∴ 。
。
又∵OB=1,OA=5,∴根据勾股定理,得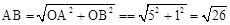 。
。
又∵BC=4,∴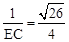 ,即
,即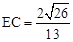 。
。
∵CF=2,∴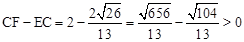 ,即
,即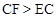 。
。
∴抛物线的对称轴与⊙C相离。
(3)存在。
假设存在满足条件的点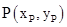 ,
,
∵点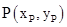 在抛物线
在抛物线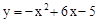 上,∴
上,∴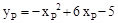 。
。
又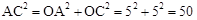 ,
,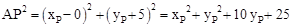 ,
,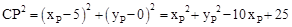 。
。
①当∠A=900时,在 中,由勾股定理,得
中,由勾股定理,得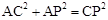 ,
,
∴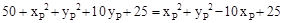 ,整理,得
,整理,得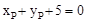 。
。
∴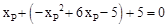 ,解得
,解得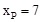 或
或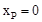 ,∴
,∴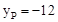 或
或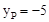 。
。
∴点P为(7,-12)或(0,-5)(舍去)。
②当∠C=900时,在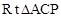 中,由勾股定理,得
中,由勾股定理,得 ,
,
∴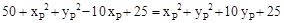 ,整理,得
,整理,得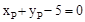 。
。
∴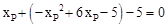 ,解得
,解得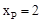 或
或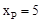 ,∴
,∴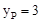 或
或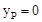 。
。
∴点P为(2,3)或(5,0)(舍去)。
综上所述,满足条件的点P的坐标为(7,-12)或(2,3)。
解析

练习册系列答案
相关题目
 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),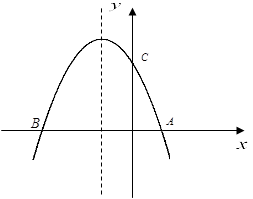
 与抛物线
与抛物线 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°, 。
。
 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数 (
( >
> )图象上,△BOC的面积为
)图象上,△BOC的面积为 .
.
 个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用
个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用 表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?  秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由. 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.


