��Ŀ����
��2013���Ĵ�����12�֣���ͼ����ֱ������ϵ�У���A������Ϊ����2��0������B������Ϊ��1��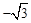 ������֪������y=ax2+bx+c��a��0����������A��B��O��OΪԭ�㣩��
������֪������y=ax2+bx+c��a��0����������A��B��O��OΪԭ�㣩��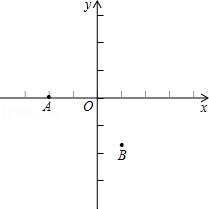
��1���������ߵĽ���ʽ��
��2���ڸ������ߵĶԳ����ϣ��Ƿ���ڵ�C��ʹ��BOC���ܳ���С�������ڣ������C�����ꣻ�������ڣ���˵�����ɣ�
��3�������P�Ǹ���������x���Ϸ���һ�����㣬��ô��PAB�Ƿ��������������У������ʱP������꼰��PAB������������û�У���˵�����ɣ���ע�⣺�����еĽ�����������ţ�
�⣺��1����A����2��0����B��1��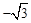 ����O��0��0��������������y=ax2+bx+c��a��0�����ã�
����O��0��0��������������y=ax2+bx+c��a��0�����ã�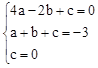 ����ã�
����ã�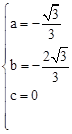 ��
��
�����������߽���ʽΪ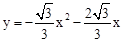 ��
��
��2�����ڡ��������£�
���ͼ����ʾ��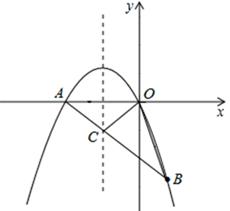
��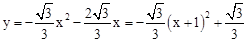 ��
��
�������ߵĶԳ���Ϊx=��1��
�ߵ�C�ڶԳ���x=��1�ϣ���BOC���ܳ�=OB+BC+CO��
��OB=2����Ҫʹ��BOC���ܳ���С������BC+CO��С��
�ߵ�O���A����ֱ��x=��1�Գƣ���CO=CA��
��BOC���ܳ�=OB+BC+CO=OB+BC+CA��
�൱A��C��B���㹲�ߣ�����CΪֱ��AB�������߶Գ���Ľ���ʱ��BC+CA��С����ʱ��BOC���ܳ���С��
��ֱ��AB�Ľ���ʽΪy=kx+t�����У�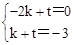 ����ã�
����ã�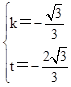 ��
��
��ֱ��AB�Ľ���ʽΪ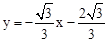 ��
��
��x=��1ʱ��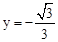 ���������C������Ϊ����1��
���������C����������1�� ����
����
��3����P��x��y������2��x��0��y��0����
��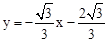 ��
��
���ͼ����ʾ������P��PQ��y���ڵ�Q��PG��x���ڵ�G������A��AF��PQ���ڵ�F������B��BE��PQ���ڵ�E����PQ=��x��PG=y��������ɵã�
 ���ٴ���ڵã�
���ٴ���ڵã�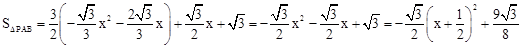 ��
��
�൱x=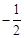 ʱ����PAB�����������ֵΪ
ʱ����PAB�����������ֵΪ ��
��
��ʱ ��
��
���P��������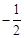 ��
�� ����
����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����������y�� ������������y��mx��ͼ����ͼ��ʾ���ɴ˿��Եõ�����
������������y��mx��ͼ����ͼ��ʾ���ɴ˿��Եõ����� ��mx��ʵ����Ϊ�� ��
��mx��ʵ����Ϊ�� ��
| A��x��-2 | B��x��1 | C��x1��2��x2����2 | D��x1��1��x2����2 |
 ������A(x1��0)��B(x2��0)��C(0����2)���䶥��ΪD.��ABΪֱ���ġ�M��y���ڵ�E��F������E����M�����߽�x���ڵ�N����ONE=30�㣬
������A(x1��0)��B(x2��0)��C(0����2)���䶥��ΪD.��ABΪֱ���ġ�M��y���ڵ�E��F������E����M�����߽�x���ڵ�N����ONE=30�㣬 ��
��
 �ϵĶ��㣨Q����E��F�غϣ�������AQ��y���ڵ�H���ʣ�AH��AQ�Ƿ�Ϊ��ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɡ�
�ϵĶ��㣨Q����E��F�غϣ�������AQ��y���ڵ�H���ʣ�AH��AQ�Ƿ�Ϊ��ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɡ�
 ��0����E��
��0����E�� �� 0����F��
�� 0����F�� ��
�� ����
����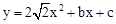 �ϣ�����������������������߽���ʽ��
�ϣ�����������������������߽���ʽ�� �ϣ���������ת�������ε�ֱ�Ƕ���P�����꣮����ֱ��д����P���������꣮
�ϣ���������ת�������ε�ֱ�Ƕ���P�����꣮����ֱ��д����P���������꣮

 ��a��0��aΪ�������Ķ������ڡ�ADE���ڲ�����a��ȡֵ��Χ��
��a��0��aΪ�������Ķ������ڡ�ADE���ڲ�����a��ȡֵ��Χ��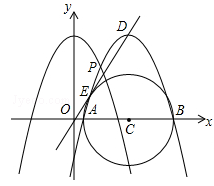

 ������A��
������A�� ��0���͵�B��1��
��0���͵�B��1�� ������x�����һ������ΪC��
������x�����һ������ΪC�� ��MFOʱ����ֱ��д���߶�BM�ij���
��MFOʱ����ֱ��д���߶�BM�ij���