题目内容
【题目】如图,直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线
点,抛物线![]() 经过点
经过点![]() 、
、![]() ,交
,交![]() 轴于另一点
轴于另一点![]() ,顶点为
,顶点为![]() .
.

![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 求点
求点![]() 、
、![]() 两点的坐标;
两点的坐标;
![]() 求
求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() ;
;![]() 的坐标为
的坐标为![]() ;(3)3.
;(3)3.
【解析】
(1)先根据直线y=x+3求出A、B两点的坐标,然后将它们代入抛物线中即可求出待定系数的值;
(2)根据(1)中抛物线的解析式可求出C,D两点的坐标;
(3)对称轴交x轴与点E,利用△ABD的面积=四边形AOBD的面积-△ABO的面积=△AED的面积+梯形OEDB的面积-△ABO的面积计算即可.
![]() 直线
直线![]() 与坐标轴的两个交点坐标分别是
与坐标轴的两个交点坐标分别是
![]() ,
,![]() ,
,
抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
![]()
![]() ,
,
得到![]() ,
,![]() ,
,
∴抛物线的解析式![]() .
.
![]() 令
令![]() ,
,
解得![]() ,
,![]() ,
,
所以![]() 点的坐标为
点的坐标为![]() ;
;
![]() ,
,
所以顶点![]() 的坐标为
的坐标为![]() .
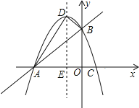
.![]() 如图,
如图,
![]() 的面积
的面积![]() 四边形
四边形![]() 的面积
的面积![]() 的面积
的面积
![]() 的面积+梯形
的面积+梯形![]() 的面积
的面积![]() 的面积
的面积
![]()
![]() .
.

练习册系列答案
相关题目
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答

①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.
【题目】己知二次函数![]() 中,函数
中,函数![]() 与自变量
与自变量![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
| 0 | 1 | 2 | 3 | 4 | … |
| … | 10 | 5 | 2 | 1 | 2 | 5 | … |
(1)求该二次函数的解析式;
(2)当![]() 为何值时,
为何值时,![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若![]() ,
,![]() 两点都在该函数的图像上,试比较
两点都在该函数的图像上,试比较![]() 与
与![]() 的大小.
的大小.





