题目内容
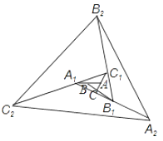
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )

A. ③④ B. ①② C. ①②③ D. ②③④
【答案】C
【解析】
由△ABC中,∠ABC与∠ACB的平分线交于点F,DE∥BC,易证得△BDF和△CEF都是等腰三角形,继而可得DE=BD+CE,又由△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;即可得△ADE的周长等于AB与AC的和.
∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵△ABC中,∠ABC与∠ACB的平分线交于点F,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
即△BDF和△CEF都是等腰三角形;
故①正确;
∴DE=DF+EF=BD+CE,
故②正确;
∴△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;
故③正确;
∵∠ABC不一定等于∠ACB,
∴∠FBC不一定等于∠FCB,
∴BF与CF不一定相等,
∴BD与CE不一定相等,故④错误.
故选:C.

练习册系列答案
相关题目
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.