Question

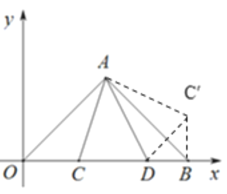
【题目】如图，在平面直角坐标系中，点B在x轴的正半轴上，AO=AB，∠OAB=90°，OB=12，点C、D均在边OB上，且∠CAD=45°，若△ACO的面积等于△ABO面积的，则点D的坐标为 _______ 。

Answer 1

【答案】（9，0）

【解析】

将△AOC绕点A逆时针旋转，使得AO和AB重合，构造出直角三角形，利用旋转的性质证明全等，通过勾股定理设出未知数列方程求解.

解：将△AOC绕点A逆时针旋转，使得AO和AB重合，旋转后点C到点C′的位置，连接C′D，

∵AO=AB，∠OAB=90°，

∴△AOB为等腰直角三角形，

∵∠CAD=45°，

∴∠C′AD=45°，

又∵AC=AC′，AD=AD

∴△ACD≌△AC′D（SAS）

∴CO=CD′

∵若△ACO的面积等于△ABO面积的，OB=12，

∴OC= BC′=4，BC=8，

∵∠AOC=∠AB C′=45°，∠ABO=45°

∴∠C′BO=90°，

设CD=x，在Rt△DBC′中，

C′D2=BD2+BC′2，

解得：x=5，

即CD=5，

∵OC=4，

所以OD=9，

∴D（9，0）