��Ŀ����
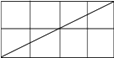
����Ŀ������m��n��m��n��1����С��������ɵľ��������У��о�����һ���Խ�����������С�����θ���f��
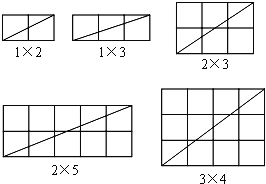
��1����m��n���ʣ�m��n��1����������������ʱ���۲�����ͼ�β�����±���
m | n | m��n | f |
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 5 | 7 | 6 |
3 | 4 | 7 | 6 |
���룺��m��n����ʱ����m��n�ľ��������У�һ���Խ�����������С�����εĸ���f��m��n�Ĺ�ϵʽ�� ������Ҫ֤������
��2����m��n������ʱ���뻭ͼ��֤�����Ĺ�ϵʽ�Ƿ���Ȼ����.
���𰸡���1��f=m��n��1����2���������۲�������ͼ�μ�����.
�������������������1��ͨ���۲켴�ɵó���m��n����ʱ����m��n�ľ��������У�һ���Խ�����������С�����εĸ���f��m��n�Ĺ�ϵʽ��
��2����m��n������ʱ������ͼ������֤����Ĺ�ϵʽ��������
�����������1��f=m��n��1��
��2����m��n������ʱ���������۲���������ͼ2��4��

��ϰ��ϵ�д�
�����Ŀ