题目内容
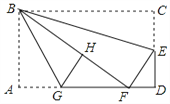
【题目】如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：① ∠EBG=45°；② AB : DE=AG : DF；③ S△ABG=
S△FGH；④ AG+DF=FG．其中正确的是_________．（填写正确结论的序号）
【答案】①③④
【解析】∵△BCE沿BE折叠，点C恰落在边AD上的点F处，∴∠1=∠2，CE=FE，BF=BC=10，
在Rt△ABF中，∵AB=6，BF=10，∴AF=
=8，∴DF=AD﹣AF=10﹣8=2，
设EF=x，则CE=x，DE=CD﹣CE=6﹣x，在Rt△DEF中，∵DE2+DF2=EF2，∴（6﹣x）2+22=x2，解得x=
，∴ED=
，
∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，∴∠3=∠4，BH=BA=6，AG=HG，
∴∠2+∠3=
∠ABC=45°，所以①正确；
HF=BF﹣BH=10﹣6=4，设AG=y，则GH=y，GF=8﹣y，
在Rt△HGF中，∵GH2+HF2=GF2，
∴y2+42=（8﹣y）2，解得y=3，∴AG=GH=3，GF=5，
∵∠A=∠D，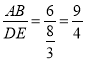 
, 
，∴
≠
，所以②错误；
∵S△ABG=
×6×3=9，S△FGH=
GHHF=
×3×4=6，
∴S△ABG=
S△FGH，所以③正确；
∵AG+DF=3+2=5，而GF=5，∴AG+DF=GF，所以④正确．
故答案为①③④．
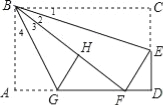
【题目】在由m×n（m×n＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，
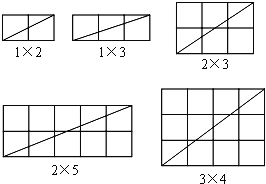
（1）当m、n互质（m、n除1外无其他公因数）时，观察下列图形并完成下表：
m | n | m＋n | f |
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 5 | 7 | 6 |
3 | 4 | 7 | 6 |
猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是 （不需要证明）；
（2）当m、n不互质时，请画图验证你猜想的关系式是否依然成立.
