题目内容
【题目】已知：二次函数y=a
＋bx＋6（a≠0）的图象与x轴交于A、B两点（点A在点B的左侧），点A、点B的横坐标是方程－4x－12=0的两个根．
（1）求出该二次函数的表达式及顶点坐标；
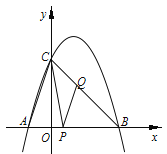
（2）如图，连接AC、BC，点P是线段OB上一个动点（点P不与点O、B重合），过点P作PQ∥AC交BC于点Q，当△CPQ的面积最大时，求点P的坐标．
【答案】(1)、y=－
＋2x＋6；(2,8)；(2)、(2,0)
【解析】
试题分析：(1)、首先求出方程的解，得出A、B两点的坐标，然后利用待定系数法求出函数解析式即顶点坐标；(2)、设点P的横坐标为m，根据△CPQ的面积得出关于m的函数关系式，然后根据二次函数的性质求出最值.
试题解析：（1）由－4x－12＝0，x＝－2或x＝6
∴A（－2，0）、B（6，0）、C（0，6）. 设二次函数y=a(－4x－12)，则：－12a＝6
∴a=－，故二次函数y=－＋2x＋6， ∴顶点坐标为：（2，8）
(2)、设点P的横坐标为m，则0＜m＜6
连结AQ，由PQ∥AC，知S△CPQ＝S△APQ＝(m＋2)·
(6－m)=－
(
－4m－12)＝－
＋6，
当m＝2时，S最大＝6 ∴当△CPQ的面积最大时，点P的坐标是（2，0）
练习册系列答案
阅读快车系列答案
相关题目
【题目】在由m×n（m×n＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，
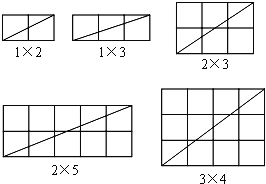
（1）当m、n互质（m、n除1外无其他公因数）时，观察下列图形并完成下表：
m | n | m＋n | f |
1 | 2 | 3 | 2 |
1 | 3 | 4 | 3 |
2 | 3 | 5 | 4 |
2 | 5 | 7 | 6 |
3 | 4 | 7 | 6 |
猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是 （不需要证明）；
（2）当m、n不互质时，请画图验证你猜想的关系式是否依然成立.