题目内容
【题目】请阅读下面材料,并回答所提出的问题.
三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
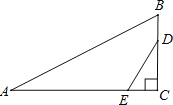
已知:如图,△ABC中,AD是角平分线.
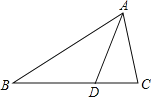
求证:![]() .
.
证明:过C作CE∥DA,交BA的延长线于E.
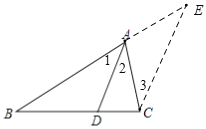
∴∠1=∠E,∠2=∠3.
∵AD是角平分线,
∴∠1=∠2.
∴∠3=∠E.
∴AC=AE.
又∵CE∥DA,
∴![]() .……①
.……①
∴![]() .
.
(1)上述证明过程中,步骤①处的理由是_____
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,则BD的长为_____cm.
【答案】平行线分线段成比例定理 ![]()
【解析】
(1)根据平行线分线段成比例定理解决问题即可.
(2)设BD=xcm,则CD=(6﹣x)cm,利用(1)中结论解决问题即可.
(1)①的理由是:平行线分线段成比例定理.
(2)设BD=xcm,则CD=(6﹣x)cm,
∵AD平分∠ABC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=![]() ,
,
∴BD=![]() cm,
cm,
故答案是:平行线分线段成比例定理,![]() .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案【题目】水库90天内的日捕捞量y(kg)与时间第x(天)满足一次函数的关系,部分数据如表:
时间第x(天) | 1 | 3 | 6 | 10 |
日捕捞量(kg) | 198 | 194 | 188 | 180 |
(1)求出y与x之间的函数解析式;
(2)水库前50天采用每天降低水位的办法减少捕捞成本,到达最低水位标准后,后40天水库维持最低水位进行捕捞.捕捞成本和时间的关系如下表:
时间第x(天) | 1≤x<50 | 50≤x≤90 |
捕捞成本(元/kg) | 60-x | 10 |
已知鲜鱼销售单价为每千克70元,假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.设销售该鲜鱼的当天收入w元(当天收入=日销售额-日捕捞成本),
①请写出w与x之间的函数解析式,并求出90天内哪天收入最大?当天收入是多少?
②若当天收入不低于4800元,请直接写出x的取值范围?