Question

【题目】如图，在矩形ABCD中，E为AD边上的一点，过C点作CF⊥CE交AB的延长线于点F.

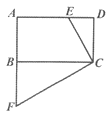
（1）求证：△CDE∽△CBF；

（2）若B为AF的中点，CB=3，DE=1，求CD的长.

Answer 1

【答案】（1）证明见解析；（2）CD=

【解析】试题分析：（1）如图，通过证明∠D=∠1，∠2=∠4即可得；

（2）由△CDE∽△CBF，可得CD：CB=DE：BF，根据B为AF中点，可得CD=BF，再根据CB=3，DE=1即可求得.

试题解析：（1）∵四边形ABCD是矩形，

∴∠D=∠1=∠2+∠3=90° ，

∵CF⊥CE，

∴∠4+∠3=90°，

∴∠2=∠4，

∴△CDE∽△CBF；

（2）∵四边形ABCD是矩形，

∴CD=AB，

∵B为AF的中点，

∴BF=AB，

∴设CD=BF=x，

∵△CDE∽△CBF，

∴，

∴ ，

∵x>0，

∴x=，

即：CD=.