Question

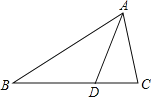
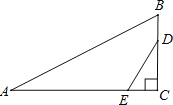
【题目】如图，在Rt△ABC中，∠C＝90°，AB＝13，BC＝5，点D、E分别在边BC、AC上，且BD＝CE，将△CDE沿DE翻折，点C落在点F处，且DF∥AB，则BD的长为_____．

Answer 1

【答案】

【解析】

根据题意作出草图，根据勾股定理求出AC，根据轴对称的性质可得EF＝CE，根据两直线平行，同位角相等可得∠A＝∠EGF，利用相似三角形对应边成比例列式表示出GE，再表示出CG，然后根据平行线分线段成比例定理列式计算即可得解．

解：如图，延长DF交AC于点G，

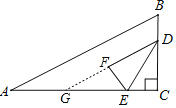
设BD＝CE＝x，

∵∠C＝90°，AB＝13，BC＝5，

∴AC＝＝＝12，

∵将△CDE沿DE翻折，点C落在点F处，

∴EF＝CE＝x，

∵DF∥AB，

∴∠A＝∠EGF，

∴△ABC∽△GEF，

∴，

即，

解得GE＝，

∴CG＝GE+CE＝，

∵DF∥AB，

∴，

即，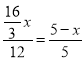

解得x＝．

即BD＝．

故答案为：．