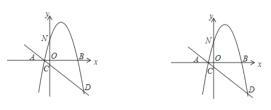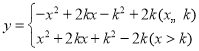题目内容
【题目】根据完全平方公式可以作如下推导（a、b都为非负数）
∵ a-2
+b=(
-
)2≥0 ∴ a-2+b≥0
∴ a+b≥2 ∴ 
≥
其实，这个不等关系可以推广，
≥
… …
（以上an都是非负数）
我们把这种关系称为：算术—几何均值不等式
例如：x为非负数时，
，则
有最小值．
再如：x为非负数时，x+x+
．
我们来研究函数：
（1）这个函数的自变量x的取值范围是 ；
（2）完成表格并在坐标系中画出这个函数的大致图象；
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
（3）根据算术—几何均值不等式，该函数在第一象限有最 值，是 ；
（4）某同学在研究这个函数时提出这样一个结论：当x>a时，y随x增大而增大,则a的取值范围是 ．
【答案】⑴ x≠0；⑵ -1，3，详见解析；⑶ 小，3 ；⑷ a≥1
【解析】
（1）根据分式的分母不能为0即可得；
（2）分别将
和代入函数的解析式可求出对应的y的值，再利用描点法画出这个函数的大致图象即可；
（3）根据算术—几何均值不等式求解即可得；
（4）根据（2）所画出的函数图象得出y随x增大而增大时，x的取值范围，由此即可得出答案．
（1）由分式的分母不能为0得：函数
的自变量x的取值范围是
故答案为：；
（2）对于函数
当时，
当时，
因此，补全表格如下：
x | … |
|
|
|
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
|
| 3 | 5 |
| … |
利用描点法画出这个函数的大致图象如下：
（3）函数在第一象限时，
由算术—几何均值不等式得：
则
有最小值，最小值为3
故答案为：小，3；
（4）由（2）的函数图象可知，当
时，y随x增大而增大
则a的取值范围是
故答案为：．
练习册系列答案
相关题目
