题目内容
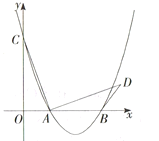
【题目】如图,在平面直角坐标系中,抛物线![]() (
(![]() 是常数,且
是常数,且![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() .连结
.连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() .当
.当![]() 最短时,
最短时,![]() 的值为_________ .
的值为_________ .
【答案】![]()
【解析】
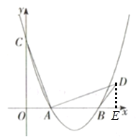
过点D作DE⊥x轴于点E,先由函数关系式求出点A、B的坐标进而求得OA、OB的长,再由旋转可得AC=AD,∠CAD=90°,由此可证得△ACO≌△DAE,进而可表示出DE和BE的长,最后利用勾股定理表示出BD2,进而即可求得当![]() 最短时的
最短时的![]() 的值.
的值.
解:如图,过点D作DE⊥x轴于点E,则∠AED=90°,
令y=0,则![]()
解得:![]() ,
,
∴OA=1,OB=3,
∴AB=OB-OA=2,
令x=0,则y=3a,
∴OC=3a,
∵旋转,
∴AC=AD,∠CAD=90°,
∴∠CAO+∠DAE=90°,
∵∠COA=90°,
∴∠CAO+∠ACO=90°,
∴∠ACO=∠DAE,
在△ACO与△DAE中,
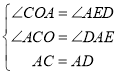
∴△ACO≌△DAE(AAS),
∴DE=OA=1,AE=OC=3a,
∴BE=AE-AB=3a-2,
∴BD2=BE2+DE2=(3a-2)2+1≥1,
当3a-2=0即a=![]() 时,BD取得最小值.
时,BD取得最小值.
故答案为:![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是 元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销![]() 件.已知产销两种产品的有关信息如下表:
件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(件) |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中![]() 为常数,且
为常数,且![]() .
.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与
与![]() 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
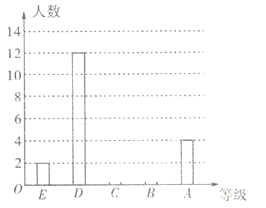
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.