题目内容
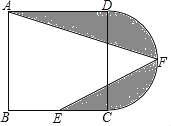
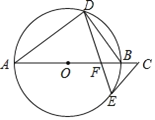
【题目】如图，AB是⊙O的直径，点D，E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
（1）求证：CE是⊙O的切线；
（2）若⊙O的半径长为5，BF=2，求EF的长．
【答案】（1）证明见解析；（2）
【解析】
（1）连接OE，易得∠ADB=90°，证明∠BOE=∠A，联立∠C=∠ABD可求证．
（2）连接BE，根据同弧所对的圆周角先证明△BEF∽△BOE，根据相似三角形的性质求出EF的长度．
解：（1）连接OE，
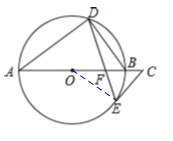
∵AB是
的直径，
∴∠ADB=90°，
∴∠A+∠ABD=90°，
由图可知∠BOE=2∠BDE
又∵∠A=2∠BDE
∴∠A=∠BOE
∵∠C=∠ABD
∴∠BOE+∠C=90°
∴OE⊥EC
∴CE是⊙O的切线．
（2）连接BE，
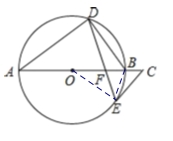
有图可知∠BED=∠A=∠BOE，
∴△BEF∽△BOE
∴
∵OB=OE=5,BF=2
∴BE=EF
∴EF2=OE·BF=10
∴EF=
故答案为：（1）证明见解析；（2）．
练习册系列答案
相关题目
【题目】根据完全平方公式可以作如下推导（a、b都为非负数）
∵ a-2
+b=(
-
)2≥0 ∴ a-2+b≥0
∴ a+b≥2 ∴ 
≥
其实，这个不等关系可以推广，
≥
… …
（以上an都是非负数）
我们把这种关系称为：算术—几何均值不等式
例如：x为非负数时，
，则
有最小值．
再如：x为非负数时，x+x+
．
我们来研究函数：
（1）这个函数的自变量x的取值范围是 ；
（2）完成表格并在坐标系中画出这个函数的大致图象；
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
（3）根据算术—几何均值不等式，该函数在第一象限有最 值，是 ；
（4）某同学在研究这个函数时提出这样一个结论：当x>a时，y随x增大而增大,则a的取值范围是 ．
