题目内容
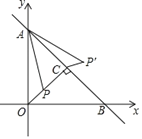
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点的直线
点的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 的另一个交点为
的另一个交点为![]() ,己知
,己知![]() ,
,![]() ,
,![]() 点为抛物线
点为抛物线![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).
(1)直接写出抛物线和直线![]() 的解析式;
的解析式;
(2)当点![]() 在直线
在直线![]() 上方的抛物线上时,连接
上方的抛物线上时,连接![]() 、
、![]() ,
,
①当![]() 的面积最大时,
的面积最大时,![]() 点的坐标是________;
点的坐标是________;
②当![]() 平分
平分![]() 时,求线段
时,求线段![]() 的长.
的长.
(3)设![]() 为直线
为直线![]() 上的点,探究是否存在点
上的点,探究是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() ,
,![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,直接写出点
为顶点的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点A、D的坐标分别代入直线表达式、抛物线的表达式,即可求解;
(2)①先找出当![]() 的面积最大时,
的面积最大时,![]() 点的位置为与直线
点的位置为与直线![]() 平行且与抛物线相切的点,设直线解析式为
平行且与抛物线相切的点,设直线解析式为![]() ,即
,即![]() 有唯一解,求出
有唯一解,求出![]() 的值,再解方程求出x、y,即为P点的坐标;②过
的值,再解方程求出x、y,即为P点的坐标;②过![]() 作
作![]() 轴于
轴于![]() 点,由
点,由![]()
![]() 先求出
先求出![]() ,根据平分线定义得
,根据平分线定义得![]() ,设
,设![]() 点坐标为
点坐标为![]() ,依题意有
,依题意有![]() ,求出t的值,进而求得PA的长;
,求出t的值,进而求得PA的长;
(3)分NC是平行四边形的一条边、NC是平行四边形的对角线,两种情况分别求解即可.
解:(1)将点![]() 、
、![]() 的坐标代入直线表达式得:
的坐标代入直线表达式得:![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:
的表达式为:![]() ,
,
将点![]() 、
、![]() 的坐标代入抛物线表达式,
的坐标代入抛物线表达式,
同理可得抛物线的表达式为:![]() ;
;
(2)①当![]() 的面积最大时,
的面积最大时,![]() 点到直线
点到直线![]() 的距离就最大,
的距离就最大,
所以![]() 点在与直线
点在与直线![]() 平行并且与抛物线相切的直线上,即
平行并且与抛物线相切的直线上,即![]() 点是这两个图像的唯一交点.
点是这两个图像的唯一交点.
设![]() 点坐标为
点坐标为![]() ,依题意有:
,依题意有:![]()
∴![]()
∵直线![]() 与抛物线相切,即只有一个交点
与抛物线相切,即只有一个交点
∴![]() ∴
∴![]()
∴![]()
∴![]() ∴
∴![]()
由此得![]() 点坐标为
点坐标为![]()
②过![]() 作
作![]() 轴于
轴于![]() 点,
点,
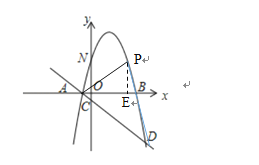
由直线![]() 的解析式
的解析式![]() ,可得
,可得![]()
![]()
∴![]()
∵![]() ∴
∴![]()
∴当![]() 平分
平分![]() 时,
时,![]() ,则
,则![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
设![]() 点坐标为
点坐标为![]() ,依题意有
,依题意有![]()
∴![]() ,
,![]() (舍去)
(舍去)
∴![]()
∴![]()
(3)![]() ,
,
①当![]() 是平行四边形的一条边时,
是平行四边形的一条边时,
设点![]() 坐标为
坐标为![]() 、则点
、则点![]() ,
,
由题意得:![]() ,即:
,即:![]() ,
,
解得:![]() 或0或4(舍去0),
或0或4(舍去0),
则:![]() 或
或![]() 或-5
或-5
则点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() ;
;
②当![]() 是平行四边形的对角线时,
是平行四边形的对角线时,
则![]() 的中点坐标为
的中点坐标为![]()
设点![]() 坐标为
坐标为![]() 、则点
、则点![]() ,
,
![]() 、
、![]() ,
,![]() 、
、![]() 为顶点的四边形为平行四边形,则
为顶点的四边形为平行四边形,则![]() 的中点即为
的中点即为![]() 中点,
中点,
即:![]() ,
,![]() ,
,
解得:![]() 或4(舍去0),d=﹣4,-d-1=3
或4(舍去0),d=﹣4,-d-1=3
故点![]() ;
;
故点M的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人数(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)这天部分出行学生使用共享单车次数的众数是_________(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |

根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.