题目内容
【题目】已知函数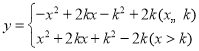 ,(
,(![]() 为常数).
为常数).
(1)当![]() 时,
时,
①求此函数图象与![]() 轴交点坐标.
轴交点坐标.
②当函数![]() 的值随
的值随![]() 的增大而增大时,自变量
的增大而增大时,自变量![]() 的取值范围为________.
的取值范围为________.
(2)若已知函数经过点(1,5),求![]() 的值,并直接写出当
的值,并直接写出当![]() 时函数
时函数![]() 的取值范围.
的取值范围.
(3)要使已知函数![]() 的取值范围内同时含有
的取值范围内同时含有![]() 和
和![]() 这四个值,直接写出
这四个值,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①(0,3);②x≤![]() 或x≥1 ;(2)
或x≥1 ;(2)![]() 或8≤y<20;(3)
或8≤y<20;(3)![]() ≤k<
≤k<![]() 或k≥2.
或k≥2.
【解析】
(1)①将![]() 代入函数关系式得
代入函数关系式得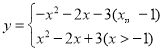 ,再将x=0代入
,再将x=0代入![]() 即可求得与y轴的交点坐标;
即可求得与y轴的交点坐标;
②先将两个二次函数关系式分别配成顶点式,再根据开口方向、对称轴及自变量的取值范围即可判断得解;
(2)将(1,5)分别代入两个函数关系式求得k的值,再逐个检验,进而可求得正确的函数关系式,再根据x的取值范围确定y的取值范围即可;
(3)分类讨论,当k≤0时,当0<k<2时,当k≥2时,画出相应的函数图像,讨论图像中的特殊点的坐标即可求得k的取值范围.
(1)当![]() 时,
时,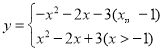
①∵![]() ,
,
∴把x=0代入![]() 得
得![]() .
.
∴此函数图象与y轴交点坐标为(0,3).
②当x≤![]() 时,
时,![]()
配方得![]()
∵a=-1<0,对称轴为直线x=-1,
∴当x≤-1,y随x的增大而增大,符合题意,
当x>![]() 时,
时,![]() ,
,
配方得![]() ,
,
∵a=1>0,对称轴为直线x=1,
∴当x≥1时,y随x的增大而增大,符合题意,
综上所述:当函数![]() 的值随
的值随![]() 的增大而增大时,自变量
的增大而增大时,自变量![]() 的取值范围为x≤
的取值范围为x≤![]() 或x≥1;
或x≥1;
(2)当k≥1时,
把(1,5)代入![]() ,得
,得![]() ,
,
解得![]() 无实根.
无实根.
当k<1时,
把(1,5)代入![]() ,得
,得![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.
∴![]() .
.
∴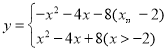
当x=-2时,将x=-2代入![]()
得:y=-4,
当-2<x≤0时,![]()
配方得![]()
∵a=1>0,对称轴为直线x=2,
∴当-2<x≤0时,8≤y<20,
综上所述:当-2≤x≤0时,y的取值范围为![]() 或8≤y<20.
或8≤y<20.
(3)由题意可知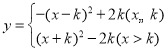 ,
,
当k≤0时,函数图像如图所示,
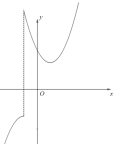
则![]() 的最大值2k≥-2即可,
的最大值2k≥-2即可,
解得k≥-1,
∴-1≤k≤0,
当0<k<2时,![]() 的最大值2k<4
的最大值2k<4
则当x>k时,![]() 的最小值<4即可,
的最小值<4即可,
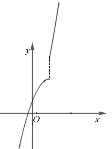
将x=k,y=4代入得![]()
解得![]() (舍去),
(舍去),
∴0<k<![]() ,
,
当k≥2时,![]() 的最大值2k≥4,
的最大值2k≥4,
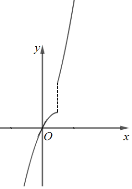
如图,此时在左边的图像上的最大值不小于4,符合题意,
∴k≥2,
综上所述:![]() ≤k<
≤k<![]() 或k≥2.
或k≥2.

 阅读快车系列答案
阅读快车系列答案【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人数(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)这天部分出行学生使用共享单车次数的众数是_________(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
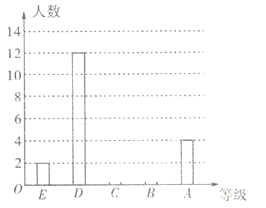
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |

根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.