题目内容
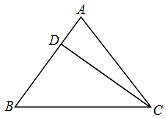
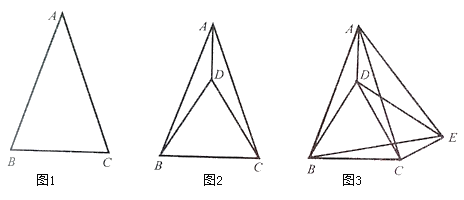
【题目】如图1,张老师在黑板上画出了一个![]() ,其中
,其中![]() ,让同学们进行探究.
,让同学们进行探究.
(1)探究一:
如图2,小明以![]() 为边在
为边在![]() 内部作等边
内部作等边![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的度数_____________;
的度数_____________;
(2)探究二:
如图3,小彬在(1)的条件下,又以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() .判断
.判断![]() 与
与![]() 的数量关系;并说明理由;
的数量关系;并说明理由;
(3)探究三:
如图3,小聪在(2)的条件下,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)150;(2)CE=AD.理由见解析;(3)![]() .
.
【解析】
(1)根据已知条件可知△ABD≌△ACD,进而得出∠ADB的度数;
(2)通过证明△ABD≌△EBC即可解答;
(3)通过前两问得出∠DCE=90°,通过角度运算得出∠BDE=90°,分别由勾股定理运算即可得.
(1)∵△BCD是等边三角形,
∴BD=BC,∠BDC=60°
∴在△ABD与△ACD中,
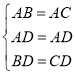
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC=![]()
故答案为:150°
(2)结论:CE=AD.
理由:∵△BDC、△ABE都是等边三角形,
∴∠ABE=∠DBC=60°,AB=BE,BD=DC,
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE,
∴∠ABD=∠EBC,
在△ABD和△EBC中
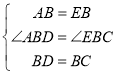 ,
,
∴△ABD≌△EBC(SAS)
∴CE=AD
(3)∵△ABD≌△EBC,
∴∠BDA=∠ECB=150°
∵∠BCD=60°,
∴∠DCE=90°.
∵∠DEC=60°,
∴∠CDE=30°
∵DE=2,
∴CE=1,
由勾股定理得:DC=BC=![]() ,
,
∵∠BDE=60°+30°=90°,DE=2,BD=![]()
由勾股定理得:BE=![]()
∵△ABE是等边三角形,
∴AE=BE=![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目