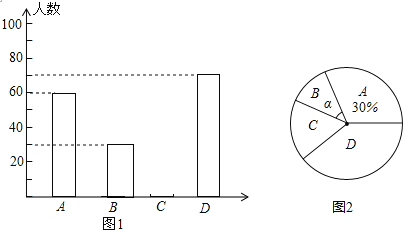
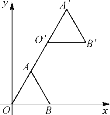
题目内容
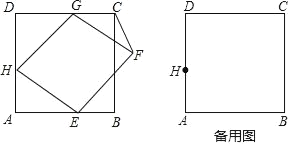
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
【答案】(1)详见解析;(2)![]() (3)60°
(3)60°
【解析】
(1)先求出HG,再判断出△AHE≌△DGH,得出∠AHE=∠DGH,进而判断出∠GHE=90,即可得出结论;
(2)先判断出∠HEA=∠FGM,进而判断出△AHE≌△MFG.得出FM=HA=1,即可得出结论;
(3)利用勾股定理依次求出GH=![]() ,AE=
,AE=![]() ,GE=
,GE=![]() ,进而判断出GH=HE=GE,即可得出结论
,进而判断出GH=HE=GE,即可得出结论
解:(1)在正方形ABCD中,
∵AH=1,
∴DH=2.
又∵DG=1,
∴HG=![]()
在△AHE和△DGH中,
∵∠A=∠D=90°,AH=DG=1,EH=HG=![]() ,
,
∴△AHE≌△DGH,
∴∠AHE=∠DGH.
∵∠DGH+∠DHG=90°,∠AHE+∠DHG=90°.
∴∠GHE=90°
所以菱形EFGH是正方形;
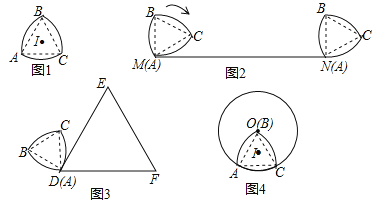
(2)如图1,过点F作FM⊥DC交DC所在直线于M,联结GE.
∵AB∥CD,
∴∠AEG=∠MGE.
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
∵∠A=∠M=90°,EH=GF.
∴△AHE≌△MFG.
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴y=![]() GCFM=
GCFM=![]() (3﹣x)×1=﹣
(3﹣x)×1=﹣![]() x+
x+![]() (0≤x≤
(0≤x≤![]() );
);
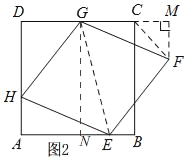
(3)如图2,当DG=![]() 时,
时,
在Rt△HDG中,DH=2,根据勾股定理得,GH=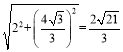 ;
;
∴HE=GH=![]() ,
,
在Rt△AEH中,根据勾股定理得,AE= ,
,
过点G作GN⊥AB于N,
∴EN=AE﹣DG=![]()
在Rt△ENG中,根据勾股定理得,GE=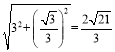
∴GH=HE=GE,
∴△GHE为等边三角形.
∴∠GHE=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
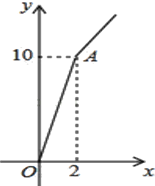
小学生10分钟应用题系列答案【题目】“十九大”之后,某种子站让利给农民,对价格为a元/千克的种子,如果一次购买2千克以上的,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象.以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
付款金额(元) | a | 7.5 | 10 | 12 | b |
购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)、指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)、求出当x>2时,y关于x的函数解析式;
(3)、甲农户将8.8元钱全部用于购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.