题目内容
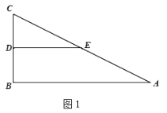
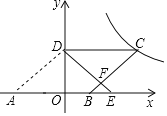
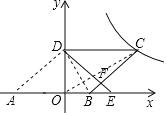
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限.将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (k≠0)图象经过点C,且S△BEF=
(k≠0)图象经过点C,且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
【答案】12
【解析】
连接OC,BD,由折叠的性质得OA=OE,由中点的性质得OA=2OB,设OB=BE=x,则OA=2x,通过证明△CDF∽△BEF,可得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,再根据三角形面积的关系即可求出k的值.
,再根据三角形面积的关系即可求出k的值.
解:连接OC,BD,
∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,
∴OA=OE,
∵点B恰好为OE的中点,
∴OE=2OB,
∴OA=2OB,
设OB=BE=x,则OA=2x,
∴AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,
∵CD∥AB,
∴△CDF∽△BEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∵S△BEF=![]() ,
,
∴S△BDF=![]() ,S△CDF=
,S△CDF=![]() ,
,
∴S△BCD=6,
∴S△CDO=S△BDC=6,
∴k=2S△CDO=12,
故答案为12.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目