题目内容
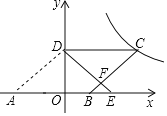
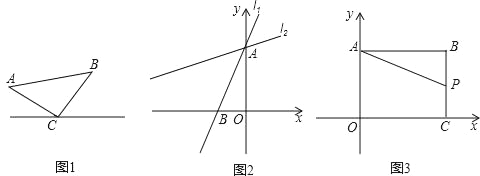
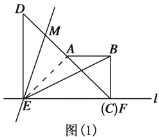
【题目】如图(1),两个等腰直角三角形ABC和DEF有一条边在同一条直线l上,DE=2,AB=1.将直线EB绕点E逆时针旋转45°,交直线AD于点M.将图(1)中的△ABC沿直线l向右平移,设C、E两点间的距离为k.请解答下列问题:
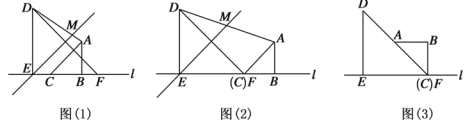
(1)①当点C与点F重合时,如图(2)所示,此时![]() 的值为 .
的值为 .
②在平移过程中,![]() 的值为 (用含k的代数式表示).
的值为 (用含k的代数式表示).
(2)将图(2)中的△ABC绕点C逆时针旋转,使点A落在线段DF上,如图(3)所示,将直线EB绕点E逆时针旋转45°,交直线AD于点M,请补全图形,并计算![]() 的值.
的值.
(3)将图(1)中的△ABC绕点C逆时针旋转α(0°<α≤45°),将直线EB绕点E逆时针旋转45°,交直线AD于点M,计算![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
【答案】(1)①1;②![]() ;(2)图详见解析,
;(2)图详见解析,![]() =1;(3)
=1;(3)![]() .
.
【解析】
(1)①当点C与点F重合时,延长BA交EM的延长线于点N,利用等腰三角形性质得出DE=AN,由此进一步证明△DEM与△AMN全等,最后进一步求出答案即可;②延长BA交EM的延长线于点N,先利用等腰三角形性质得出EC=AN=![]() ,然后证明△DEM与△ANM相似,据此进一步求出答案即可;
,然后证明△DEM与△ANM相似,据此进一步求出答案即可;
(2)连接AE,先证明△AEM与△FEB相似,由此进一步利用相似三角形性质求出答案即可;
(3)过点B作BG⊥BE,交直线EM于点G,连接AG,先证明△AGM与△DEM相似,由此进一步利用相似三角形性质求出答案即可.
(1)①当点C与点F重合时,如下图,延长BA交EM的延长线于点N,
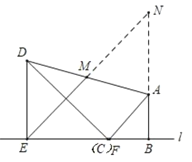
由题意得可得:∠NEB=45°,∠ABE=90°,
∴△EBN是等腰直角三角形,
∴BE=BN,
∵△ABC是等腰三角形,
∴AB=BC,
∴AN=EC,
又∵△DEF是等腰三角形,
∴DE=EF,
∴AN=EC=DE,
∵DE∥AN,
∴∠DEN=∠N,
在△DME与△AMN中,
∵∠DME=∠AMN,∠DEN=∠N,DE=AN,
∴△DEM△AMN(AAS),
∴DM=AM,
∴![]() ;
;
②如图,延长BA交EM的延长线于点N,
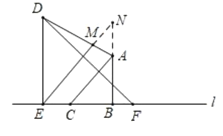
由题意得可得:∠NEB=45°,∠ABE=90°,
∴△EBN是等腰直角三角形,
∴BE=BN,
∵△ABC是等腰三角形,
∴AB=BC,
∴EC=AN=![]() ,
,
∵DE∥AN,
∴△DEM~△ANM,
∴![]()
故答案为:①1,②![]() ;
;
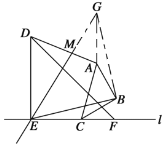
(2)补全如图所示,连接AE,
∵△ABC、△DEF均为等腰直角三角形,DE=2,AB=1,
∴EF=2,BC=1,∠DEF=90°,∠DFE=∠ACB=45°,
∴DF=2![]() ,AC=
,AC=![]() ,∠EFB=90°,
,∠EFB=90°,
∴DF=2AC,AD=![]() ,
,
∵点A为CD的中点,
∴EA⊥DF,EA平分∠DEF,
∴∠MAE=90°,∠AEF=45°,AE=![]() ,
,
∵∠BEM=45°,
∴∠MEA+∠AEB=∠BEF+∠AEB=45°,
∴∠MEA=∠BEF,
∴△AEM~△FEB,
∴![]() ,
,
∴AM=![]() ,
,
∴DM=AD-AM=![]() ,
,
∴![]() =1;
=1;
(3)如图,过点B作BG⊥BE,交直线EM于点G,连接AG,
∴∠EBG=90°,
∵∠BEM=45°,
∴∠EGB=45°,
∴BE=BG,
∵△ABC为等腰直角三角形,
∴BA=BC,∠ABC=90°,
∴∠ABG=∠CBE,
∴△ABG△CBE,
∴AG=EC=![]() ,∠AGB=∠CEB,
,∠AGB=∠CEB,
∵∠AGB+∠AGE=∠DEM+∠CEB=45°,
∴∠AGE=∠DEM,
∴AG∥DE,
∴△AGM~△DEM,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某文具商店销售学习用品,已知某品牌钢笔的进价是20元,销售过程发现,每月销量y支与销售单价x元(x为正整数)之间满足一次函数关系,且每支钢笔的售价不低于进价,也不高于35元,下表是y与x之间的对应数据:
销售单价x(元) | … | 22 | 24 | 30 | … |
月销量y(只) | … | 92 | 84 | 60 | … |
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每支钢笔的售价定为多少元时,月销售利润恰为600元?
(3)每支钢笔的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
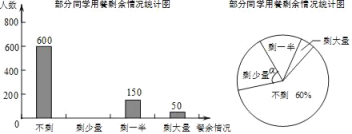
【题目】小明和小红为了更直观了解“物体质量”的概念,各选五个鸡蛋称重,以每个![]() 为标准,大于或等于
为标准,大于或等于![]() 即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:
即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:![]() ).
).
序号 数据 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小红 |
|
|
| 2 | 1 |
经过统计发现,小明所选鸡蛋质量的平均数为![]() ,小红所选鸡蛋质量的众数为
,小红所选鸡蛋质量的众数为![]() ,根据以上信息:
,根据以上信息:
(1)填空:![]() ,
,![]() ;
;
(2)通过计算说明,小明和小红哪个选取的鸡蛋大小更均匀,请说明理由;
(3)现从小明和小红所选取的鸡蛋里各随机挑一个,这两个鸡蛋质量都达标的概率是多少?