题目内容
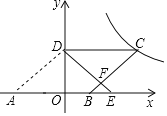
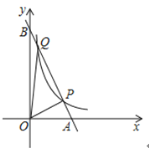
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ; (2)相等.理由见解析;(3)
; (2)相等.理由见解析;(3)![]() .
.
【解析】
(1)利用待定系数法即可解决问题.
(2)利用三角形的面积公式求出三角形的面积即可判断.
(3)如图作点Q关于y轴的对称点Q’,理解PQ’交y轴于M,参数MQ+MP的值最小.求出最小PQ’的解析式即可解决问题.
解:(1)∵反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则有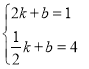 ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)相等.
理由:∵![]()
∴当![]() 时,
时,![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,
,![]()
∴![]() .
.
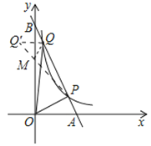
(3)如图作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,理解
,理解![]() 交
交![]() 轴于
轴于![]() ,参数
,参数![]() 的值最小.
的值最小.
∵![]() ,
,
∴![]() ,
,
直线![]() 的解析式为
的解析式为![]() ,则有
,则有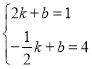 ,6
,6
解得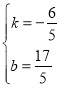 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目