Question

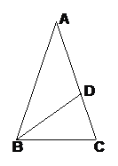
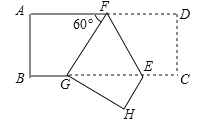
【题目】如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为且∠AFG=60°，GE=2BG，则折痕EF的长为（ ）

A. 1 B. C. 2 D.

Answer 1

【答案】C

【解析】

试题解析：由折叠的性质可知，DF=GF，HE=CE，GH=DC，∠DFE=∠GFE．

∵∠GFE+∠DFE=180°﹣∠AFG=120°，∴∠GFE=60°．

∵AF∥GE，∠AFG=60°，∴∠FGE=∠AFG=60°，∴△GEF为等边三角形，∴EF=GE．

∵∠FGE=60°，∠FGE+∠HGE=90°，∴∠HGE=30°．

在Rt△GHE中，∠HGE=30°，∴GE=2HE=CE，∴GH==HE=CE．

∵GE=2BG，∴BC=BG+GE+EC=4EC．

∵矩形ABCD的面积为，∴4ECEC=，∴EC=1，EF=GE=2．

故选C．