МвДҝДЪИЭ
ЎҫМвДҝЎҝОКМвФӯРНЈәФЪНјўЩөДҫШРОMNPQЦРЈ¬өгEЎўFЎўGЎўH·ЦұрФЪNPЎўPQЎўQMЎўMNЙПЈ¬ИфЎП1=ЎП2=ЎП3=ЎП4Ј¬ФтіЖЛДұЯРОEFGHОӘҫШРОMNPQөД·ҙЙдЛДұЯРОЈ®
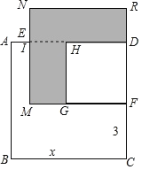
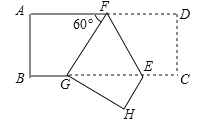
ІЩЧчУлМҪҫҝЈәФЪНјўЪЈ¬НјўЫөДҫШРОABCDЦРЈ¬AB=4Ј¬BC=8өгEЎўF·ЦұрФЪBCЎўCDұЯЙПЈ¬КФАыУГХэ·ҪРОНшёс·ЦұрЧчіцБҪНјЦРҫШРОABCDөД·ҙЙдЛДұЯРОEFGHЈ¬ІўЗуіцГҝёц·ҙЙдЛДұЯРОEFGHөДЦЬіӨЈ®
·ўПЦУлУҰУГЈәУЙЗ°ГжөДІЩЧчҝЙТФ·ўПЦТ»ёцҫШРОУРІ»Н¬өД·ҙЙдЛДұЯРОЈ¬ЗТХвР©·ҙЙдЛДұЯРОөДЦЬіӨ¶јПаөИЈ¬ИфФЪНјўЩҫШРОMNPQЦРЈ¬MN=3Ј¬NP=4ФтЖд·ҙЙдЛДұЯРОEFGHөДЦЬіӨОӘЎЎЎЎЈ®

Ўҫҙр°ёЎҝ(1)јыҪвОцЈ»ЈЁ2Ј©8![]() Ј»ЈЁ3Ј©10
Ј»ЈЁ3Ј©10
ЎҫҪвОцЎҝ
(1)ЎўёщҫЭ·ҙЙдЛДұЯРОөДә¬ТеәНEЎўFөгөДО»ЦГ»ӯіцјҙҝЙЈ»(2)ЎўёщҫЭ№ҙ№Й¶ЁАнЗуіцұЯіӨЈ¬јҙҝЙЗуіцЦЬіӨЈ»(3)ЎўСУіӨGHҪ»PNөДСУіӨПЯУЪөгAЈ¬№эөгGЧчGKЎНNPУЪKЈ¬ЦӨГчRtЎчFPEәНRtЎчFPBИ«өИЈ¬ҙУ¶шЗуіцGBөДіӨ¶ИЈ¬ёщҫЭЛДұЯРОЦЬіӨөИУЪ2GBөГіцҙр°ёЈ®
ЈЁ1Ј©ЧчНјИзПВЈә
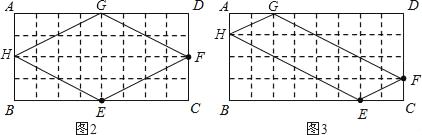
ЈЁ2Ј©ФЪНј2ЦРЈ¬EF=FG=GH=HE=![]() =2
=2![]() Ј¬ЎаЛДұЯРОEFGHөДЦЬіӨОӘ4ЎБ2
Ј¬ЎаЛДұЯРОEFGHөДЦЬіӨОӘ4ЎБ2![]() =8
=8![]() Ј¬
Ј¬
ФЪНј3ЦРЈ¬EF=GH=![]() Ј¬FG=HE=
Ј¬FG=HE=![]() =3
=3![]() Ј¬
Ј¬
ЎаЛДұЯРОEFGHөДЦЬіӨОӘ2ЎБ![]() +2ЎБ3
+2ЎБ3![]() =2
=2![]() +6
+6![]() =8
=8![]() Ј®
Ј®
ЈЁ3Ј©ИзНј4Ј¬СУіӨGHҪ»PNөДСУіӨПЯУЪөгAЈ¬№эөгGЧчGKЎНNPУЪKЈ¬
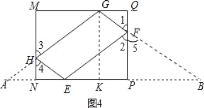
ЎЯЎП1=ЎП2Ј¬ЎП1=ЎП5Ј¬ЎаЎП2=ЎП5Ј®
ФЪЎчFPEәНЎчFPBЦРЈ¬ Ј¬ЎаRtЎчFPEЎХRtЎчFPBЈЁASAЈ©Ј¬ЎаEF=BFЈ¬EP=PBЈ¬
Ј¬ЎаRtЎчFPEЎХRtЎчFPBЈЁASAЈ©Ј¬ЎаEF=BFЈ¬EP=PBЈ¬
Н¬АнЈәAH=EHЈ¬NA=ENЈ®ЎаAB=2NP=8Ј®ЎЯЎПB=90Ўг©ҒЎП5=90Ўг©ҒЎП1Ј¬ЎПA=90Ўг©ҒЎП3Ј¬
ЎаЎПA=ЎПBЈ®ЎаGA=GBЈ®ФтKB=![]() AB=4Ј¬ЎаGB=
AB=4Ј¬ЎаGB=![]() =5Ј¬
=5Ј¬
ЎаЛДұЯРОEFGHөДЦЬіӨОӘЈә2GB=10Ј®

 ҝЪЛгДЬКЦПөБРҙр°ё
ҝЪЛгДЬКЦПөБРҙр°ё