题目内容
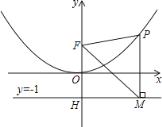
【题目】如图所示,二次函数图象的顶点在原点O,且经过点(1,![]() ).点F(0,1)在y轴上.直线y=-1与y轴交于点H.
).点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求该二次函数的解析式;
(2)设点P是(1)中图象上在第一象限内的动点,过点P作x轴的垂线与直线y=-1交于点M.
①求证:FM平分∠OFP;
②当△FPM是等边三角形时,试求P点的坐标.
【答案】(1)y=![]() x2;(2)①详见解析;②点P的坐标为(2
x2;(2)①详见解析;②点P的坐标为(2![]() ,3).
,3).
【解析】
(1)根据二次函数图象的顶点在原点O,设二次函数的解析式为![]() ,将
,将![]() 代入即可求出解析式;
代入即可求出解析式;
(2)①过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,![]() ,结合平行线的性质,可得出结论.
,结合平行线的性质,可得出结论.
②根据△FPM是等边三角形,可得∠PMF=60°,∴∠FMH=30°,设P点坐标为![]() ,根据PF=PM=FM,可得关于
,根据PF=PM=FM,可得关于![]() 的方程,求出
的方程,求出![]() 的值,即可等得出答案.
的值,即可等得出答案.
(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为![]() ,
,
将点![]() 代入
代入![]() 得
得![]() ,
,
∴二次函数的解析式为![]() .
.

(2)①证明:∵点P在抛物线![]() 上,
上,
∴可设点P的坐标为![]() ,
,
如右图,过点P作PB⊥y轴于点B,
则![]() ,
,![]() ,
,
∴Rt△BPF中,![]() ,
,
∵PM⊥直线![]() ,∴
,∴![]() ,
,
∴PF=PM.
∴∠PFM=∠PMF,
又∵PM∥![]() 轴,∴∠MFH=∠PMF,
轴,∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP.
②当△FPM是等边三角形时,∠PMF=60°,∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,∴![]() ,
,
解得:![]() ,(舍去-2
,(舍去-2![]() )
)
∴![]() ,
,
∴满足条件的点P的坐标为(2![]() ,3).
,3).

练习册系列答案
相关题目