题目内容
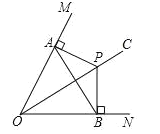
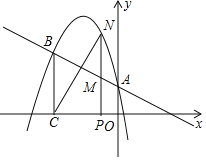
【题目】如图所示,二次函数y=ax2﹣![]() x+c的图象经过点A(0,1),B(﹣3,
x+c的图象经过点A(0,1),B(﹣3, ![]() ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
【答案】(1)y=﹣![]() x+1;y=﹣
x+1;y=﹣![]() x2﹣
x2﹣![]() x+1;(2)当m=﹣
x+1;(2)当m=﹣![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]() ;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
【解析】试题分析:(1)根据已知点的坐标利用待定系数法即可得出结论;
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]() 用含
用含![]() 的代数式表示出来
的代数式表示出来![]() ,结合二次函数的性质即可解决最值问题;
,结合二次函数的性质即可解决最值问题;
(3)假设存在,设点N的坐标为![]() 连接
连接![]() ,当四边形
,当四边形![]() 为菱形时,
为菱形时, ![]() 与
与![]() 相互垂直平分,根据
相互垂直平分,根据![]() 算出
算出![]() 的值,从而得出点
的值,从而得出点![]() 的坐标,再去验证
的坐标,再去验证![]() 是否等于
是否等于![]() ,由此即可得出结论.
,由此即可得出结论.
试题解析:(1)设直线AB的解析式为:y=kx+b,
∴
∴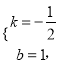
∴直线AB的解析式为: ![]()
把![]() 代入
代入![]() 得,
得, 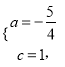
∴二次函数的解析式为: ![]()
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]()
![]()
∴当![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]()
(3)假设存在,设点N的坐标为![]() 连接BN、CM,如图所示.
连接BN、CM,如图所示.
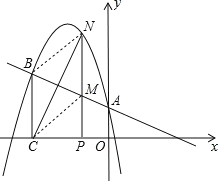
若要BM与NC相互垂直平分,只需四边形BCMN为菱形即可。
∵点B坐标为![]() 点C的坐标为(3,0),
点C的坐标为(3,0),
∴BC=52.
∵四边形BCMN为菱形,
![]() 解得:
解得: ![]()
当m=2时,点N的坐标为![]()
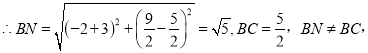
故m=2(舍去);
当m=1时,点N的坐标为(1,4),
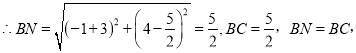
∴点N(1,4)符合题意.
故存在点N,使得BM与NC相互垂直平分,点N的坐标为(1,4).

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目