题目内容
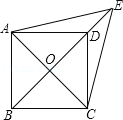
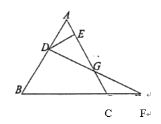
【题目】如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
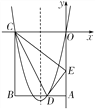
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的表达式;
(3)一动点P从点C 出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E 点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t s,当t为何值时,DP=DQ.
【答案】(1)3(2) y=![]() x2+
x2+![]() x;(3)
x;(3)![]()
【解析】
(1)在Rt△COE中,OE=![]() ;
;
(2)在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m,求得:O,D,C的坐标,再代入解析式,可解得;
(3)由CP=2t,BP=5-2t,和BD=DE=![]() ,再证Rt△DBP≌Rt△DEQ,得BP=EQ.可求得t.
,再证Rt△DBP≌Rt△DEQ,得BP=EQ.可求得t.
解:(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,
OE=![]() =3;
=3;
(2)设AD=m,则DE=BD=4-m,
∵OE=3,∴AE=5-3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m=![]() ,
,
∴D![]() ,∵C(-4,0),O(0,0),
,∵C(-4,0),O(0,0),
∴设过O,D,C三点的抛物线为y=ax(x+4),
∴-5=![]() ,解得a=
,解得a=![]() ,
,
∴抛物线表达式为y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(3)∵CP=2t,∴BP=5-2t,
由折叠的性质,得BD=DE=![]() ,
,
在Rt△DBP和Rt△DEQ中,![]() ,
,
∴Rt△DBP≌Rt△DEQ(HL)
∴BP=EQ,
∴5-2t=t,∴t=![]() .
.

练习册系列答案
相关题目