题目内容
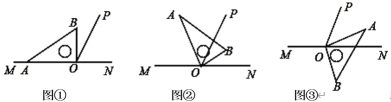
【题目】① 如图（1），直线l上有2个点，则图中有2条可用图中字母表示的射线：A1A2、A2A1，有1条线段：A1A2；
② 如图（2），直线l上有3个点，则图中有几条可用图中字母表示的射线，有几条线段，并分别用图中字母表示出来；
③ 如图（3），直线l上有n个点，则图中有多少条可用图中字母表示的射线，有多少条线段，分别用含n的代数式表示出来；
④ 应用（3）中发现的规律解决问题：某校七年级共有8个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需多少场比赛？
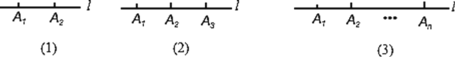
【答案】②射线有4条，线段有3条；③射线的条数是(2n-2)条，线段的条数是
条；④ 28场．
【解析】
②写出所有的射线和线段后再计算个数；
③根据规律，射线是每个点为端点的射线有两条，但是两边的两个点只有一条；
线段是从所有点中任取两个；
④根据题意8个队每两个队之间塞一场，和已知点数确定线段数同理，所以代入求值即可．
解：②根据射线的定义可得：射线有，A1A2、A2A3、A2A1、A3A1，共4条；由线段的定义可得线段有：射线有，A1A2、A2A3、A2A1、A3A1，共3条；
③根据规律，射线是每个点用两次，但第一个和最后一个只用一次，所以射线的条数是2n-2，线段是从这些点中任取两个点就是一条线段，所以线段的条数是；
④∵某校七年级共有8个班进行足球比赛，
∴全部赛完共需比赛场次为：
（场），
∴全部赛完共需比赛场次为28.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
