Question

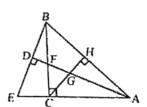
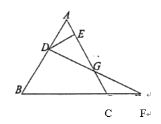
【题目】如图，在边长为1的等边△ABC的边AB取一点D，过点D作DE⊥AC于点E，在BC延长线取一点F，使CF=AD，连接DF交AC于点G，则EG的长为________

Answer 1

【答案】

【解析】

过D作BC的平行线交AC于H，通过求证△DHG和△FCG全等，推出HG=CG，再通过证明△ADH是等边三角形和DE⊥AC，推出AE=EH，即可推出AE+GC=EH+HG，可得EG=AC，即可推出EG的长度．

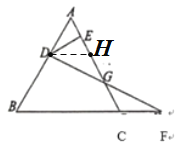
解：如图，过D作DH∥BC，交AC于点H.

∴∠F=∠GDH，

∵△ABC是等边三角形，

∴∠ADH=∠B=60°，∠AHD=∠ACB=60°，

∴△ADH是等边三角形，

∴AD=DH，

∵AD=CF，

∴DH=CF，

∵∠DGH=∠FGC，

∴△DGH≌△FGC（AAS），

∴HG=CG.

∵DE⊥AC，△ADH是等边三角形，

∴AE=EH，

∴AE+CG=EH+HG，

∴EG=AC=；

故答案为：.