题目内容
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

【答案】⑴![]() ⑵存在AP=
⑵存在AP=![]() ⑶ 存在,∠PBQ=45°
⑶ 存在,∠PBQ=45°
【解析】(1)根据∠PBC+∠ABP=∠ABP+∠APB=90°得出∠APB=∠PBC ,再由tan∠PBC=tan∠APB=4=![]() ;(2) 延长PQ交BC延长线于点E.设PD=x,由 ∠PBC=∠BPQ ,可得EB=EP ,再由△PDQ≌△ECQ 得到QP=
;(2) 延长PQ交BC延长线于点E.设PD=x,由 ∠PBC=∠BPQ ,可得EB=EP ,再由△PDQ≌△ECQ 得到QP=![]() ,在Rt△PDQ中根据勾股定理可得出结论;(3) 作BH⊥PQ于
,在Rt△PDQ中根据勾股定理可得出结论;(3) 作BH⊥PQ于![]() 点,易证,△PAB≌△PHB,可得∠PBH=
点,易证,△PAB≌△PHB,可得∠PBH=![]() ∠ABH,再由 Rt△BHQ≌Rt△BCQ,可得∠HBQ=
∠ABH,再由 Rt△BHQ≌Rt△BCQ,可得∠HBQ=![]() ∠HBC,进而得出结论即可.
∠HBC,进而得出结论即可.
(1)∵∠PBC+∠ABP=∠ABP+∠APB=90°, ∴∠APB=∠PBC=90°,在RT△ABP中,tan∠PBC=tan∠APB=4=![]() ;
;
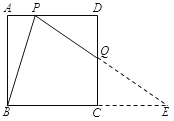
⑵如图1,存在![]()
延长PQ交BC延长线于点E.设PD=x.
∵∠PBC=∠BPQ,
∴EB=EP.
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DPQ=∠E,.
在△PDQ和△ECQ中,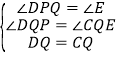 ,
,
∴△PDQ≌△ECQ(AAS).
∴PD=CE,PQ=QE. ∴BE=EP=![]() , ∴QP=
, ∴QP=![]() .
.
在Rt△PDQ中,∵PD2+QD2=PQ2,
∴![]() ,解得
,解得![]()
∴AP=AD﹣PD=![]() .
.
⑶存在,∠PBQ=45°.作![]() 于
于![]() 点.
点.
易证,△PAB≌△PHB,
∴∠ABP=∠HBP, ∴∠PBH=![]() ∠ABH.
∠ABH.
易证,Rt△BHQ≌Rt△BCQ,
∴∠HBQ=∠CBQ, ∴∠HBQ=![]() ∠HBC,
∠HBC,
∴∠PBQ=∠PBH+∠HBQ=![]() (∠ABH+∠HBC)=
(∠ABH+∠HBC)=![]() ∠ABC=45°.
∠ABC=45°.