题目内容
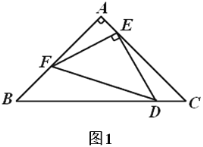
【题目】已知:在菱形 ABCD 中,点 E 是 CD 边上一点,过点 E 作 EF AC 于点 F,交 BC 边于点 G, 交 AB 延长线于点 H.
(1)如图 1,求证:BH=DE;
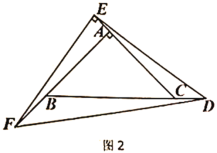
(2)如图 2,当点 E 是 CD 边中点时,连接对角线 BD 交对角线 AC 于点 O,连接 OG、OE,在不添加任何辅助线和字母的情况下,请直接写出图 2 中所有的平行四边形(菱形除外).
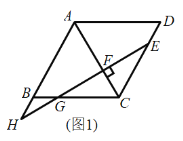
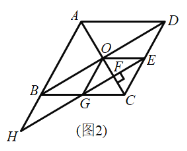
【答案】(1)证明见解析;(2)平行四边形BHED,平行四边形BHGO,平行四边形OGED,平行四边形OBGE.
【解析】
(1)证△GFC≌△EFC(ASA),得出CG=CE,∠CGF=∠CEF,证出∠H=∠BGH,得出BH=BG,进而得出结论;
(2)由菱形的性质和三角形中位线定理即可得出答案.
(1)证明:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,AC平分∠BCD,
∴∠GCF=∠ECF,
∵EF⊥AC,
∴∠GFC=∠EFC=90°,
在△GFC和△EFC中,
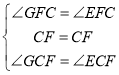 ,
,
∴△GFC≌△EFC(ASA),
∴CG=CE,∠CGF=∠CEF,
∵AB∥CD,
∴∠H=∠CEF,
∵∠BGH=∠CGF,
∴∠H=∠BGH,
∴BH=BG,
∵BC=CD,CG=CE,
∴BC-CG=CD-CE,
即BG=DE;
(2)所有的平行四边形(菱形除外)为平行四边形BHED、平行四边形BHGO、平行四边形OGED、平行四边形OBGE;
理由如下:
∵四边形ABCD是菱形,
∴AB∥CD,
由(1)得:CG=CE,BH=BG=DE,
∴四边形BHED为平行四边形,
∵点E是CD边中点,BC=CD,
∴CE=DE=BG=CG,
∵四边形ABCD是菱形,
∴AB∥CD,OB=OD,
∴OE、OG都是△BCD的中位线,
∴OE∥BG,OG∥CD∥AB,OG=![]() CD=DE=BH,OE=
CD=DE=BH,OE=![]() BC=BG,
BC=BG,
∴四边形OBGE、四边形BHGO、四边形OGED都是平行四边形.

【题目】某厂的四台机床同时生产直径为![]() 的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:
的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:![]() ):
):
特征数 机床 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 9.99 | 9.99 | 10.00 | 0.02 |
乙 | 9.99 | 10.00 | 10.00 | 0.07 |
丙 | 10.02 | 10.01 | 10.00 | 0.02 |
丁 | 10.02 | 9.99 | 10.00 | 0.05 |
从样本来看,生产的零件直径更接近标准要求且更稳定的机床是( )
A.甲B.乙C.丙D.丁