题目内容
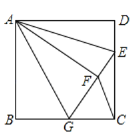
【题目】矩形ABCD中,AB=4,BC=8,折叠ABCD使点A与点C重合,折痕为EF,则EF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设BE=x,表示出CE=8x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.
如图,
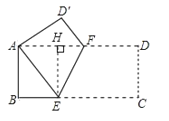
设BE=x,则CE=BCBE=8x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=8x,
在Rt△ABE中,AB2+BE2=AE2,
即42+x2=(8x)2
解得x=3,
∴AE=83=5,
由翻折的性质得,∠AEF=∠CEF,
∵矩形ABCD的对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=5,
过点E作EH⊥AD于H,则四边形ABEH是矩形,
∴EH=AB=4,
AH=BE=3,
∴FH=AFAH=53=2,
在Rt△EFH中,EF=![]() ,
,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
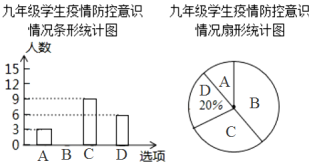
【题目】在某项比赛中,已知不同小组的甲、乙两队的五次预选赛成绩(每次比赛的成绩为0分,10分,20分三种情况)分别如下列不完整的统计表及条形统计图所示.
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 | x | 20 |
乙队五次预选赛成绩条形统计图
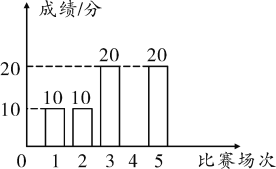
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)求出乙第四次预选赛的成绩;
(2)求甲队成绩的平均数及x的值;
(3)从甲、乙两队前3次比赛中随机各选择一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.