题目内容
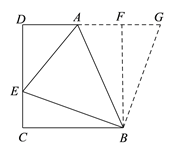
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.

【答案】6
【解析】如下图,过点B作BF⊥DA交DA的延长线于点F,延长AF到G,使FG=CE=2,连接BG,
∴∠BFD=∠BFG=90°,
∵AD∥BC,∠D=90°,
∴∠C=90°,
∵DC=BC,
∴四边形BCDF是正方形,
∴BF=BC,∠CBF=90°,
又∵∠C=∠BFG=90°,CE=FG,
∴△BCE≌△BFG,
∴BF=BG,∠CBE=∠FBG,
∵∠ABE=45°,
∴∠CBE+∠ABF=45°,即∠ABG=45°,
∴∠ABE=∠ABG,
又∵AB=AB,
∴△ABE≌△ABG,
∴AG=AE=5,
∴AF=5-2=3,
设BC=x,则CD=AF=x,
∴DE=x-1,AD=x-3,
∵在Rt△ADE中,DE2+AD2=AE2,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),
∴BC=6.
故答案为6.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目