题目内容
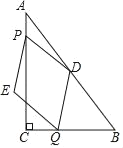
【题目】正方形ABCD的边长为3,点E在直线CD上,且DE=1,连接BE,作AF⊥BE于点H,交直线BC于点F,连接EF,则EF的长是_________.
【答案】![]() 或
或![]()
【解析】
分两种情况:当E在CD的延长线上时,当E在线段CD上时.通过条件证得△ABF≌△BCE,然后得到EC和CF的长,即可解答.
解:如图,当E在CD的延长线上时,
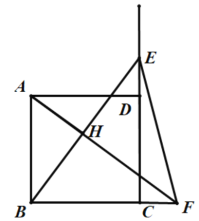
由题意可知,AB=BC=3,∠ABC=∠BCD=90°,DE=1,
∴∠HBC+∠BEC=90°,CE=3+1=4,
∵AF⊥BE,
∴∠HBC+∠BFA=90°,
∴∠BFA=∠BEC,
在△ABF和△BCE中,
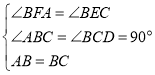
∴△ABF≌△BCE,
∴BF=CE=4,
∴CF=4-3=1,
∴![]() ,
,
如图,当E在线段CD上时,
同第一种情况可得△ABF≌△BCE,
∴BF=CE=3-1=2,
∴CF=3-2=1,
∴![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】今年是全面建成小康社会和“十三五”规划收官之年,为促进销售,某公司开发了A、B两项新产品,销售前景广阔.已知A、B的成本、售价和每日销量如下表所示:
成本(元/件) | 售价(元/件) | 销量(件/日) | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
根据销售情况,公司对B项产品降价销售,同时对A项产品提价销售,发现B项产品每降价5元就多销售2件,A项产品每提价5元就可少销售1件,要保持每日的总销量不变,设A项产品每天少销售x个,每天总获利为y元.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)要使每天利润不低于208000元,直接写出x的取值范围;
(3)该公司决定每销售一件A产品,就捐给红十字会a(0<a≤100)元作为抗疫基金.当40≤x≤50时,每日的最大利润为237250元,求a的值.