题目内容
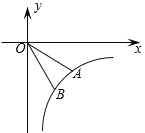
【题目】如图，点A、点B是双曲线y＝
上的两点，OA＝OB＝6，sin∠AOB＝
，则k＝___．
【答案】
【解析】
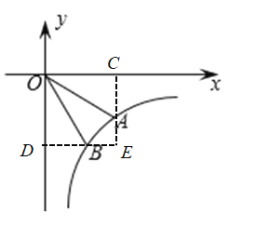
分别过点A、B作y轴和x轴的垂线，垂足分别为C、D，相交于E，设A点坐标为（a，b），则B、D点坐标为（b，a）和（a，a）,AC=BD=|a-b|；由两点间距离公式得a2+b2=36以及反比例函数图像的特征得ab=k，二者联立解得a2=18±
；然后根据反比例函数图像的特征、三角函数的应用、坐标的应用，表示出SODEC、S△OAC、S△OBD、S△OAB、S△AEB的面积，然后SODEC=S△OAC+S△OBD+S△OAB+S△AEB列出方程，最后分a2=18+ 和a2=18-两种情况解答即可．
解：分别过点A、B作y轴和x轴的垂线，垂足分别为C、D，相交于E
设A点坐标为（a，b），则B、D点坐标为（b，a）和（a，a）,AC=BD=|a-b|
∵OA=6
∴a2+b2=36，即b2=36- a2
∵点A、点B是双曲线y＝
上的两点
∴S△OAC=S△OBD=
|k|，ab=|k|，
∴
解得：a2=18±
∵sin∠AOB＝
∴S△OAB=
∴S△AEB=
=18-|k|
∵SODEC=S△OAC+S△OBD+S△OAB+S△AEB=a2
∴|k|+6+18-|k|= a2，整理为a2=24
①当a2=18＋，即6=，即的|k|=12
∵函数图像在二四象限
∴k=-12
②a2=18-，即6=-无意义
故答案为：-12.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】今年是全面建成小康社会和“十三五”规划收官之年，为促进销售，某公司开发了A、B两项新产品，销售前景广阔．已知A、B的成本、售价和每日销量如下表所示：
成本（元/件） | 售价（元/件） | 销量（件/日） | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
根据销售情况，公司对B项产品降价销售，同时对A项产品提价销售，发现B项产品每降价5元就多销售2件，A项产品每提价5元就可少销售1件，要保持每日的总销量不变，设A项产品每天少销售x个，每天总获利为y元．
（1）求y与x的函数关系式，并写出x的取值范围；
（2）要使每天利润不低于208000元，直接写出x的取值范围；
（3）该公司决定每销售一件A产品，就捐给红十字会a（0＜a≤100）元作为抗疫基金．当40≤x≤50时，每日的最大利润为237250元，求a的值．
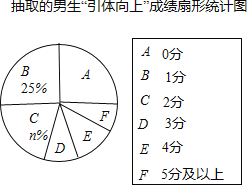
【题目】某市明年的初中毕业升学考试，拟将“引体向上”作为男生体育考试的一个必考项目，满分为10分．有关部门为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平，在全市八年级男生中随机抽取了部分男生，对他们的“引体向上”水平进行测试，并将测试结果绘制成如下统计图表（部分信息未给出）：
请你根据统计图表中的信息，解答下列问题：
抽取的男生“引体向上”成绩统计表
成绩 | 人数 |
0分 | 32 |
1分 | 30 |
2分 | 24 |
3分 | 11 |
4分 | 15 |
5分及以上 | m |
（1）填空：m＝ ，n＝ ．
（2）求扇形统计图中D组的扇形圆心角的度数；
（3）目前该市八年级有男生3600名，请估计其中“引体向上”得零分的人数．
