题目内容
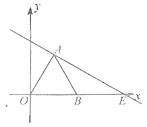
【题目】已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED的度数为（ ）
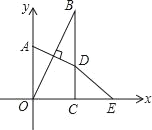
A.10°B.20°C.30°D.35°
【答案】B
【解析】
先根据平行线的性质求出∠AOB的度数，由直角三角形的性质得出∠BOC的度数，再根据点A关于直线OB的对称点D恰好在BC上得出OB是线段AD的垂直平分线，故可得出∠BOD的度数，进而得出∠DOC的度数，由点E与点O关于直线BC对称可知BC是OE的垂直平分线，故可得出∠DOC=∠OED．
解：连接OD，
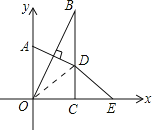
∵BC⊥x轴于点C，∠OBC=35°，
∴∠AOB=∠OBC=35°，∠BOC=90°-35°=55°．
∵点A关于直线OB的对称点D恰好在BC上，
∴OB是线段AD的垂直平分线，
∴∠BOD=∠AOB=35°，
∴∠DOC=∠BOC-∠BOD=55°-35°=20°．
∵点E与点O关于直线BC对称，
∴BC是OE的垂直平分线，
∴∠DOC=∠OED=20°．
故选：B．
练习册系列答案
相关题目
