题目内容
【题目】已知
，点
在
的内部，
，在
、
上分别取点
、
，使
的周长最短，则
周长的最小值为（ ）
A.4B.8C.16D.32
【答案】B
【解析】
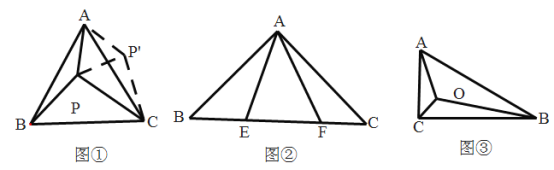
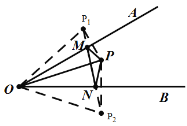
分别作点P关于OA、OB的对称点P1、P2，连接P1P2，交OA于点M，交OB于点N，则此时
周长的最小值等于线段P1P2，只要证明△OP1P2为等边三角形，即可求解.
解：如图，分别作点P关于OA、OB的对称点P1、P2，连接P1P2，交OA于点M，交OB于点N，
根据轴对称的性质，则
OP1=OP=OP2，∠P1OA=∠POA，∠P2OB=∠POB，MP=MP1，NP=NP2,
∴△PMN的周长的最小值= P1P2，
∵
，
∴∠P1OP2=2∠AOB=60°，
∴△OP1P2为等边三角形，
∴P1P2=OP1=OP2=OP=8；
故选择：B.
练习册系列答案
相关题目
