题目内容
【题目】如图,在平面直角坐标系中,△OAB是边长为2的等边三角形过点A的直线![]() 与
与![]() 轴交于点E,
轴交于点E,
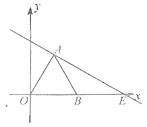
(1)求点E坐标。
(2)求过A,O,E三点的抛物线表达式。
(3)若P是(2)中求出的抛物线AE段上的一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值。
【答案】(1)E(4,0);(2)![]() ;(3)S最大值=
;(3)S最大值=![]() .
.
【解析】
试题(1)应用锐角三角函数求出点A的坐标,而后求出一次函数解析式,求出直线与x轴的交点E的坐标;
(2)应用待定系数法列出方程组,求出a、b、c的值,得到二次函数解析式;
(3)设点![]() ,根据
,根据![]() 用点P的坐标表示面积,整理得到S=
用点P的坐标表示面积,整理得到S=![]() ,即当
,即当![]() 时,
时,![]() .
.
试题解析:解:(1)作AF⊥x轴与F,
∴OF=OAcos60°=1,AF=OFtan60°=![]() ,
,
∴点A(1,![]() ),
),
代入直线解析式,得![]() ,∴m=
,∴m=![]() ,
,
∴![]() ,
,
当y=0时,![]() ,
,
得x=4,
∴点E(4,0);

(2)设过A、O、E三点抛物线的解析式为![]() ,
,
∵抛物线过原点,
∴c=0,
∴![]() ,
,
∴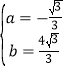 ,
,
∴抛物线的解析式为![]() ;
;
(3)作PG⊥x轴于G,设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() .
.

【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.