题目内容
【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，△ABC绕点C顺时针旋转一定角度得到△DEC，点D恰好落在AB边上，连接AE. 求：
（1）旋转角的度数；
（2）AE的长度.
【答案】（1）60°；（2）
.
【解析】
（1）由旋转的性质可知AC=DC， BC=EC，∠ACB=∠DCE=90°.证△ACD是等边三角形，可得∠ACD=60°,即旋转角的度数为60°；（2）连接BE，证△BCE是等边三角形.
求出BE=BC=
，∠CBE=60°，由勾股定理可得：
.
（1）∵∠ACB=90°，∠ABC=30°，AC=1，
∴∠BAC=90°-∠ABC=60°，AB=2AC=2，BC=
.
由旋转的性质可知AC=DC， BC=EC，∠ACB=∠DCE=90°.
∵CA=CD，∠BAC=60°，
∴△ACD是等边三角形.
∴∠ACD=60°,即旋转角的度数为60°.
（2）连接BE，
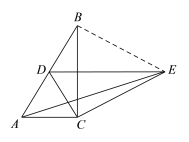
由（1），得∠BCD=30°.
∴∠BCE=60°.
∵BC=EC,
∴△BCE是等边三角形.
∴BE=BC=，∠CBE=60°.
∵∠ABE=∠ABC+∠CBE=90°，
∴.
【题目】随着地铁和共享单车的发展，“地铁
单车”已成为很多市民出行的选择
张老师从学校站出发，先乘坐地铁到某一站出地铁，再骑共享单车回家，设他出地铁的站点与学校距离为
单位：千米
，乘坐地铁的时间为
单位分钟，经测量，得到如下数据：
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
根据表中数据的规律，直接写出表格中a、b的值和
关于x的函数表达式；
张老师骑单车的时间
单位：分钟也受x的影响，其关系可以用
米描述，
若张老师出地铁的站点与学校距离为14千米，请求出张老师从学校回到家所需的时间；
若张老师准备在离家较近的A，B，C，D，E中的某一站出地铁，请问：张老师应选择在哪一站出地铁，才能使他从学校回到家所需的时间最短？并求出最短时间．
