Question

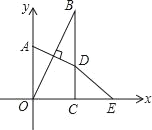
【题目】如图，△ABC中，CD为AB边上的高，AD＝8，CD＝4，BD＝3．动点P从点A出发，沿射线AB运动，速度为1个单位/秒，运动时间为t秒．

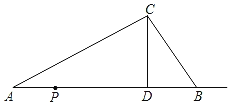
（1）当t为何值时，△PDC≌△BDC；

（2）当t为何值时，△PBC是等腰三角形？

Answer 1

【答案】（1）t的值为5或11；（2）t＝

【解析】

(1)由于△PDC≌△BDC,可得PD=BD，分PD＝BD＝3或点P与B重合，两种情况构建方程即可得出结论:

(2)分PD＝BD＝3或BC＝BP＝5， 或CP＝BP时，可三种情况讨论，由等腰三角形的性质和勾股定理可求解.

解：（1）∵△PDC≌△BDC，

∴PD＝BD＝3，即8﹣t＝3，解得t＝5（秒）；

或点P与B重合，此时t＝11，

综上所述，满足条件的t的值为5或11；

（2）∵CD＝4，BD＝3，CD⊥AB，

当BC＝CP时，且CD⊥AB，

∴PD＝BD＝3，可得8﹣t＝3，解得t＝5（秒）；

当BC＝BP＝5，可得11﹣t＝5，解得t＝6（秒）；

当CP＝BP时，可得CP2＝PD2+CD2，

∴BP2＝（BP﹣3）2+16，

∴t＝