题目内容
【题目】在正方形![]() 中,
中,![]() 为正方形的外角
为正方形的外角![]() 的角平分线,点
的角平分线,点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
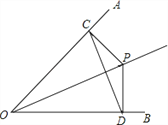
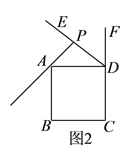
(![]() )如图1,若点
)如图1,若点![]() 与点
与点![]() 重合.
重合.
①依题意补全图1.
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
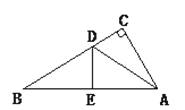
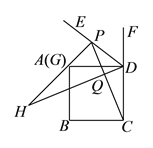
(![]() )如图2,若点
)如图2,若点![]() 恰好在线段
恰好在线段![]() 上,正方形
上,正方形![]() 的边长为
的边长为![]() ,请写出求
,请写出求![]() 长的思路(可以不写出计算结果).
长的思路(可以不写出计算结果).

【答案】(![]() )①补图见解析;②
)①补图见解析;②![]() ,证明见解析;(
,证明见解析;(![]() )思路见解析.
)思路见解析.
【解析】试题分析:(![]() )①依题意补全图形即可;
)①依题意补全图形即可;
② 通过证明![]() 与
与![]() 全等即可得到DH与PC的关系;
全等即可得到DH与PC的关系;
(![]() )通过证明
)通过证明![]() ,
,![]() ,从而可得
,从而可得![]() ,继而得到
,继而得到![]() ,通过计算即可得.
,通过计算即可得.
试题解析:(![]() )①如图所示:
)①如图所示:
②![]() ,理由如下:
,理由如下:
∵![]() 为正方形的外角
为正方形的外角![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )a.与②同理得:
)a.与②同理得:![]() ,
,![]() ,
,
则![]() .
.
b.由②可知![]() 为等腰直角三角形,可得
为等腰直角三角形,可得
![]() ,故
,故![]() 为等腰直角三角形,
为等腰直角三角形,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
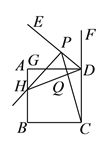
c.由![]() 得
得![]() ,
,
即![]() ,
,
可得出![]() (舍负),
(舍负),
则![]() .
.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目