题目内容
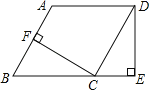
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
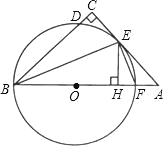
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF;(3)由(2)中CD=HF,即可求出HF的值,先求OA和OF的长度,再由AF=OA-OF求出AF的值;
试题解析:
(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;
(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF
证明:(1)如图,连接OE.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)如图,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
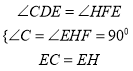 ,
,
∴△CDE≌△HFE(AAS),
∴CD=HF.
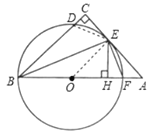
(3)由(2)得,CD=HF.又CD=1
∴HF=1
在Rt△HFE中,EF=![]() =
=![]()
∵EF⊥BE
∴∠BEF=90°
∴∠EHF=∠BEF=90°
∵∠EFH=∠BFE
∴△EHF∽△BEF
∴![]() ,即
,即![]()
∴BF=10
∴![]() ,
, ![]() ,
,
∴在Rt△OHE中, ![]() ,
,
∴在Rt△EOA中, ![]() ,
,
∴![]()
∴![]()
∴![]() .
.