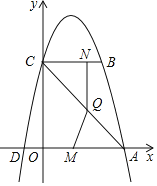��Ŀ����
����Ŀ��ijҽҩ�о�������ijһ���Ʋ�����ҩ�Ŀ��������������ķ��������֪�������˰��涨�ļ������ú�ÿ����ѪҺ�к�ҩ��y�ˣ�1��=10-3���ˣ���ʱ��xСʱ�ı仯������ijһ�����κ���y=ax2+bx+c (a��0)���Ǻϣ�����÷���ʱ����ʱ��Ϊ0ʱ��ÿ����ѪҺ�к�ҩ��Ϊ0�ˣ����ú�2Сʱÿ����ѪҺ�к�ҩ��Ϊ6�ˣ����ú�3Сʱ��ÿ����ѪҺ�к�ҩ��Ϊ7.5�ˣ�
��1�������ҩ��y���ˣ����ҩʱ��x��Сʱ���ĺ�����ϵʽ��������0��x��8�ڵĺ�����ͼ���ʾ��ͼ��
��2�����ҩ��Сʱ����ʹÿ����ѪҺ�к�ҩ��������ѪҺ�е����ҩ����
��3�����ͼ��˵��һ�η�ҩ�����Чʱ���Ƕ���Сʱ������Чʱ��ΪѪҺ�к�ҩ����Ϊ0����ʱ�䣩
���𰸡���1��![]() ��ͼ�����������2����ҩ��4Сʱ������ʹѪҺ�к�ҩ�������ʱÿ����ѪҺ�к���ҩҺ8�ˣ���3��һ�η�ҩ�����Чʱ��Ϊ8Сʱ
��ͼ�����������2����ҩ��4Сʱ������ʹѪҺ�к�ҩ�������ʱÿ����ѪҺ�к���ҩҺ8�ˣ���3��һ�η�ҩ�����Чʱ��Ϊ8Сʱ
��������
��1�����ݴ���ϵ��������3��������ɷ����鼴����ý���ʽ��
��2��ͨ���䷽�����������ֵ��
��3��ʹy=0���������x��ֵ��������xֵ��ľ���ֵ��ʱЧ
��1����y=ax2+bx+c����
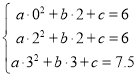
��ã�a=-![]() �� b=4�� c=0��
�� b=4�� c=0��
��y=��![]() x2+4x��ͼ�����£�
x2+4x��ͼ�����£�
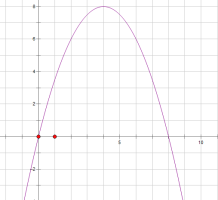
��2��y=��![]() x2+4x=-
x2+4x=-![]() (x-4)2+8��
(x-4)2+8��
���ҩ��4Сʱ������ʹѪҺ�к�ҩ�������ʱÿ����ѪҺ�к���ҩҺ8�ˣ�
��3����y=0ʱ��x1=0��x2=8����һ�η�ҩ�����Чʱ��Ϊ8Сʱ��

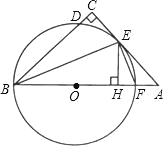
����Ŀ����֤������֪����ͼ��![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ����ʱ����λͬѧ��֤�����£�
����ʱ����λͬѧ��֤�����£�
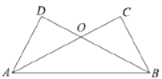
֤��һ���ɹ��ɶ�������
|
֤������
|
��1����˼��������λͬѧ��֤���У���һλͬѧ����ɵ�֤��������һ��������Ѵ������д����
��2������ѡ������һ��֤�������֤����
����Ŀ��2018��ijʡʵʩ�˲��������ߣ��������˲Ÿ����ʽ���ֺ��仧�Żݣ�������Ӣ�ŷ�����֯���ŵݽ���������Ϊ���˽ⱨ����Ա����ṹ���������������50��������Ա�����䣨��λ���꣩���������õ������ݷֳ�5�飬ͳ�����±���
���� | Ƶ���������� | Ƶ�� |
30������ | 0.16 | |
����30�겻����40�� | 20 | 0.40 |
����40�겻����50�� | 14 | |
����50�겻����60�� | 6 | 0.12 |
60������ |
��1���뽫�����пո���д������
��2���������ݵ���λ������_____���������������Ƴ�����ͳ��ͼ������30�겻����40�ꡱ��Բ�Ľ�Ϊ______�ȣ�
��3���������2000�˱�������������������ݣ��������䲻����40��ı�����Ա���ж����ˣ�