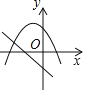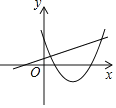ЬтФПФкШн
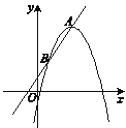
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() КЭХзЮяЯпWНЛгкAЃЌBСНЕуЃЌЦфжаЕуAЪЧХзЮяЯпWЕФЖЅЕуЃЎЕБЕуAдкжБЯп
КЭХзЮяЯпWНЛгкAЃЌBСНЕуЃЌЦфжаЕуAЪЧХзЮяЯпWЕФЖЅЕуЃЎЕБЕуAдкжБЯп![]() ЩЯдЫЖЏЪБЃЌХзЮяЯпWЫцЕуAзїЦНвЦдЫЖЏЃЎдкХзЮяЯпЦНвЦЕФЙ§ГЬжаЃЌЯпЖЮABЕФГЄЖШБЃГжВЛБфЃЎ
ЩЯдЫЖЏЪБЃЌХзЮяЯпWЫцЕуAзїЦНвЦдЫЖЏЃЎдкХзЮяЯпЦНвЦЕФЙ§ГЬжаЃЌЯпЖЮABЕФГЄЖШБЃГжВЛБфЃЎ
гІгУЩЯУцЕФНсТлЃЌНтОіЯТСаЮЪЬтЃК
дкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊжБЯп![]() ЃЎЕуAЪЧжБЯп
ЃЎЕуAЪЧжБЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЧвЕуAЕФКсзјБъЮЊ
ЩЯЕФвЛИіЖЏЕуЃЌЧвЕуAЕФКсзјБъЮЊ![]() ЃЎвдAЮЊЖЅЕуЕФХзЮяЯп
ЃЎвдAЮЊЖЅЕуЕФХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ЕФСэвЛИіНЛЕуЮЊЕуBЃЎ
ЕФСэвЛИіНЛЕуЮЊЕуBЃЎ
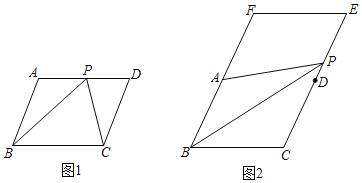
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓХзЮяЯп
ЪБЃЌЧѓХзЮяЯп![]() ЕФНтЮіЪНКЭABЕФГЄЃЛ
ЕФНтЮіЪНКЭABЕФГЄЃЛ
ЃЈ2ЃЉЕБЕуBЕНжБЯпOAЕФОрРыДяЕНзюДѓЪБЃЌжБНгаДГіДЫЪБЕуAЕФзјБъЃЛ
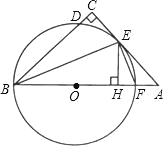
ЃЈ3ЃЉЙ§ЕуAзїДЙжБгк![]() жсЕФжБЯпНЛжБЯп
жсЕФжБЯпНЛжБЯп![]() гкЕуCЃЎвдCЮЊЖЅЕуЕФХзЮяЯп
гкЕуCЃЎвдCЮЊЖЅЕуЕФХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ЕФСэвЛИіНЛЕуЮЊЕуDЃЎ
ЕФСэвЛИіНЛЕуЮЊЕуDЃЎ
ЂйЕБACЁЭBDЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкШєвдAЃЌBЃЌCЃЌDЮЊЖЅЕуЙЙГЩЕФЭМаЮЪЧЭЙЫФБпаЮЃЈИїИіФкНЧЖШЪ§ЖМаЁгк180ЁуЃЉЪБЃЌжБНгаДГіТњзуЬѕМўЕФ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнt=0ЪБЃЌAЕФзјБъПЩвдЧѓЕУЪЧЃЈ0ЃЌ-2ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУХзЮяЯпЕФНтЮіЪНЃЌдђBЕФзјБъПЩвдЧѓЕУЃЛ
ЃЈ2ЃЉЁїOABЕФУцЛ§вЛЖЈЃЌЕБOAзюаЁЪБЃЌBЕНOAЕФОрРыМДЁїOABжаOAБпЩЯЕФИпзюДѓЃЌДЫЪБOAЁЭABЃЌОнДЫМДПЩЧѓНтЃЛ
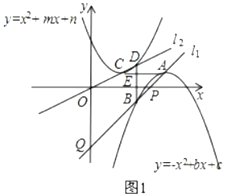
ЃЈ3ЃЉЂйЗНЗЈвЛЃКЩшACЃЌBDНЛгкЕуEЃЌжБЯпl1ЃКy=x-2ЃЌгыxжсЁЂyжсНЛгкЕуPКЭQЃЈШчЭМ1ЃЉЃЎгЩЕуDдкХзЮяЯпC2ЃКy=[x-ЃЈ2t-4ЃЉ]2+ЃЈt-2ЃЉЩЯЃЌПЩЕУ![]() =[ЃЈt-1ЃЉ-ЃЈ2t-4ЃЉ]2+ЃЈt-2ЃЉЃЌНтЗНГЬМДПЩЕУЕНtЕФжЕЃЛ
=[ЃЈt-1ЃЉ-ЃЈ2t-4ЃЉ]2+ЃЈt-2ЃЉЃЌНтЗНГЬМДПЩЕУЕНtЕФжЕЃЛ
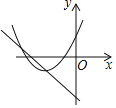
ЗНЗЈЖўЃКЩшжБЯпl1ЃКy=x-2гыxжсНЛгкЕуPЃЌЙ§ЕуAзїyжсЕФЦНааЯпЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌНЛгкЕуNЃЎЃЈШчЭМ2ЃЉЃЌИљОнBDЁЭACЃЌПЩЕУt-1=2t-![]() ЃЌНтЗНГЬМДПЩЕУЕНtЕФжЕЃЛ
ЃЌНтЗНГЬМДПЩЕУЕНtЕФжЕЃЛ
ЂкЩшжБЯпl1гыl2НЛгкЕуMЃЎЫцзХЕуAДгзѓЯђгвдЫЖЏЃЌДгЕуDгыЕуMжиКЯЃЌЕНЕуBгыЕуMжиКЯЕФЙ§ГЬжаЃЌПЩЕУТњзуЬѕМўЕФtЕФШЁжЕЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉЁпЕуAдкжБЯпl1ЃКy=x-2ЩЯЃЌЧвЕуAЕФКсзјБъЮЊ0ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈ0ЃЌ-2ЃЉЃЌ
ЁрХзЮяЯпC1ЕФНтЮіЪНЮЊy=-x2-2ЃЌ
ЁпЕуBдкжБЯпl1ЃКy=x-2ЩЯЃЌ
ЩшЕуBЕФзјБъЮЊЃЈxЃЌx-2ЃЉЃЎ
ЁпЕуBдкХзЮяЯпC1ЃКy=-x2-2ЩЯЃЌ
Ёрx-2=-x2-2ЃЌ
НтЕУx=0Лђx=-1ЃЎ
ЁпЕуAгыЕуBВЛжиКЯЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ-1ЃЌ-3ЃЉЃЌ
ЁргЩЙДЙЩЖЈРэЕУAB=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЕБOAЁЭABЪБЃЌЕуBЕНжБЯпOAЕФОрРыДяЕНзюДѓЃЌдђOAЕФНтЮіЪНЪЧy=-xЃЌдђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
дђЕуAЕФзјБъЮЊЃЈ1ЃЌ-1ЃЉЃЎ
ЃЈ3ЃЉЂйЗНЗЈвЛЃКЩш![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌгы
ЃЌгы![]() жсЁЂ
жсЁЂ![]() жсНЛгкЕу
жсНЛгкЕу![]() КЭ
КЭ![]() ЃЈШчЭМ1ЃЉЃЎ
ЃЈШчЭМ1ЃЉЃЎ
дђЕу![]() КЭЕу
КЭЕу![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЎ
ЃЎ
Ёп![]() жсЃЌ
жсЃЌ
Ёр![]() жсЃЎ
жсЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧвЕу
ЩЯЃЌЧвЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
Ёп![]() жсЃЌ
жсЃЌ
ЁрЕу![]() ЕФзнзјБъЮЊ
ЕФзнзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁрХзЮяЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁпЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ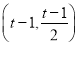 ЃЎ
ЃЎ
ЁпЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЎ
ЃЎ
НтЕУ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁпЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌ
жиКЯЃЌ
Ёр![]()
ЗНЗЈЖўЃКЩшжБЯпl1ЃКy=x-2гыxжсНЛгкЕуPЃЌЙ§ЕуAзїyжсЕФЦНааЯпЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌНЛгкЕуNЃЎЃЈШчЭМ2ЃЉ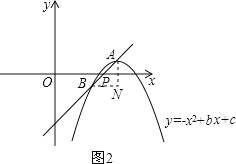
дђЁЯANB=90ЁуЃЌЁЯABN=ЁЯOPBЃЎ
дкЁїABNжаЃЌBN=ABcosЁЯABNЃЌAN=ABsinЁЯABNЃЎ
ЁпдкХзЮяЯпC1ЫцЖЅЕуAЦНвЦЕФЙ§ГЬжаЃЌ
ABЕФГЄЖШВЛБфЃЌЁЯABNЕФДѓаЁВЛБфЃЌ
ЁрBNКЭANЕФГЄЖШвВВЛБфЃЌМДЕуAгыЕуBЕФКсзјБъЕФВювдМАзнзјБъЕФВюЖМБЃГжВЛБфЃЎ
ЭЌРэЃЌЕуCгыЕуDЕФКсзјБъЕФВювдМАзнзјБъЕФВювВБЃГжВЛБфЃЎ
гЩЃЈ1ЃЉжЊЕБЕуAЕФзјБъЮЊЃЈ0ЃЌ-2ЃЉЪБЃЌЕуBЕФзјБъЮЊЃЈ-1ЃЌ-3ЃЉЃЌ
ЁрЕБЕуAЕФзјБъЮЊЃЈtЃЌt-2ЃЉЪБЃЌЕуBЕФзјБъЮЊЃЈt-1ЃЌt-3ЃЉЃЎ
ЁпACЁЮxжсЃЌ
ЁрЕуCЕФзнзјБъЮЊt-2ЃЎ
ЁпЕуCдкжБЯпl2ЃКyЃН![]() xЩЯЃЌ
xЩЯЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ2t-4ЃЌt-2ЃЉЃЎ
Сюt=2ЃЌдђЕуCЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЃЎ
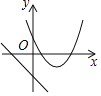
ЁрХзЮяЯпC2ЕФНтЮіЪНЮЊy=x2ЃЎ
ЁпЕуDдкжБЯпl2ЃКyЃН![]() xЩЯЃЌ
xЩЯЃЌ
ЁрЩшЕуDЕФзјБъЮЊ(xЃЌ![]() )ЃЎ
)ЃЎ
ЁпЕуDдкХзЮяЯпC2ЃКy=x2ЩЯЃЌ
Ёр![]() ЃНx2ЃЎ
ЃНx2ЃЎ
НтЕУxЃН![]() Лђx=0ЃЎ
Лђx=0ЃЎ
ЁпЕуCгыЕуDВЛжиКЯЃЌ
ЁрЕуDЕФзјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ЁрЕБЕуCЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЪБЃЌЕуDЕФзјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ЁрЕБЕуCЕФзјБъЮЊЃЈ2t-4ЃЌt-2ЃЉЪБЃЌЕуDЕФзјБъЮЊ(2t![]() ЃЌt
ЃЌt![]() )ЃЎ
)ЃЎ
ЁпBDЁЭACЃЌ
Ёрt1ЃН2t![]() ЃЎ
ЃЎ
ЁрtЃН![]() ЃЎ
ЃЎ
ЂкtЕФШЁжЕЗЖЮЇЪЧtЃМ![]() ЛђtЃО5ЃЎ
ЛђtЃО5ЃЎ
ЩшжБЯпl1гыl2НЛгкЕуMЃЎЫцзХЕуAДгзѓЯђгвдЫЖЏЃЌДгЕуDгыЕуMжиКЯЃЌЕНЕуBгыЕуMжиКЯЕФЙ§ГЬжаЃЌвдAЃЌBЃЌCЃЌDЮЊЖЅЕуЙЙГЩЕФЭМаЮВЛЪЧЭЙЫФБпаЮЃЎ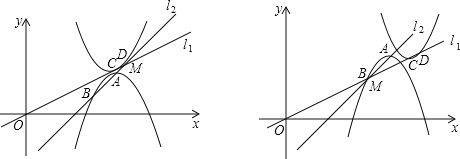

 бєЙтЪдОэЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтЪдОэЕЅдЊВтЪдОэЯЕСаД№АИ