Question

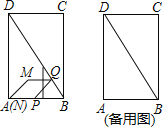
【题目】已知如图，在正方形ABCD中，AD=4，E，F分别是CD，BC上的一点，且∠EAF=45°，EC=1，将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合，连接EF，过点B作BM∥AG，交AF于点M，则以下结论：①DE+BF=EF，②BF=，③AF=，④S△MEF=中正确的是　　

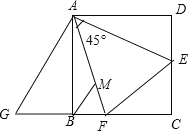
A. ①②③ B. ②③④ C. ①③④ D. ①②④

Answer 1

【答案】D

【解析】

利用全等三角形的性质条件勾股定理求出的长，再利用相似三角形的性质求出△BMF的面积即可

解: ∵AG=AE, ∠FAE=∠FAG=45°,AF=AF,

∴△AFE △AFG,

∴EF=FG

∵DE=BG

∴EF=FG=BG+FB=DE+BF故①正确

∵BC=CD=AD=4，EC=1

∴DE=3，设BF=x，则EF=x+3,CF=4-x,

在Rt△ECF中，（x+3）2=（4-x）2+12

解得x=

∴BF= ,AF= 故②正确，③错误，

∵BM∥AG

∴△FBM~△FGA

∴

∴S△MEF=，故④正确，

故选：D．