题目内容
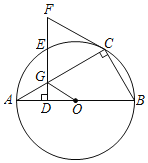
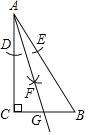
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,按下列步骤作图:①以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E;②分别以D,E为圆心,DE的长为半径画弧,两弧相交于点F;③作射线AF,交BC于点G,则CG=( )
A.3B.6C.![]() D.
D.![]()
【答案】D
【解析】
作GH⊥AB于H,如图,由基本作图得到AG平分∠CAB,则GH=GC,利用勾股定理计算出AB=10,利用△ACG≌△AHG得到AH=AC=8,则BH=10﹣8=2,设GC=x,则BG=6﹣x,根据勾股定理得到22+x2=(6﹣x)2,然后解方程即可.
解:作GH⊥AB于H,如图,
由作法得AG平分∠CAB,
∵GC⊥AC,GH⊥AB,
∴GH=GC,
在Rt△ABC中,AB=![]() =10,
=10,
易得△ACG≌△AHG,
∴AH=AC=8,
∴BH=10﹣8=2,
设GC=x,则BG=6﹣x,
在Rt△BGH中,22+x2=(6﹣x)2,解得x=![]() ,
,
即CG的长为![]() .
.
故选:D.

练习册系列答案
相关题目