Question

【题目】我们定义:如果两个等腰三角形的顶角相等，且项角的顶点互相重合，则称此图形为“手拉手全等模型”.因为顶点相连的四条边，形象的可以看作两双手，所以通常称为“手拉手模型”.例如，如（1），与都是等腰三角形，其中，则△ABD≌△ACE(SAS).

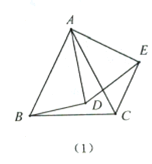
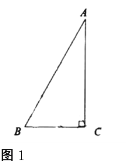
（1）熟悉模型：如（2），已知与都是等腰三角形，AB=AC，AD=AE，且，求证:；

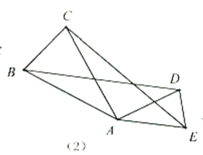
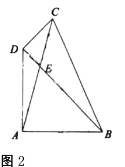
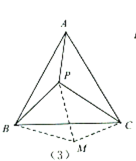
（2）运用模型：如（3），为等边内一点，且，求的度数.小明在解决此问题时，根据前面的“手拉手全等模型”，以为边构造等边，这样就有两个等边三角形共顶点，然后连结，通过转化的思想求出了的度数，则的度数为 度；

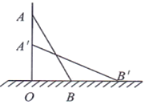
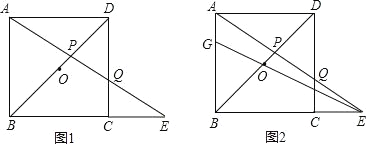
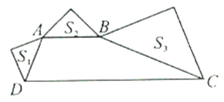
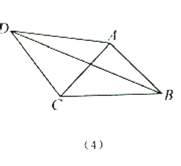
（3）深化模型:如（4），在四边形中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，求的长.

Answer 1

【答案】（1）见解析；（2）150°；（3）

【解析】

（1）根据“SAS”证明△ABD≌△ACE即可；

（2）根据小明的构造方法，通过证明△BAP≌△BMC，可证∠BPA=∠BMC，AP=CM，根据勾股定理的逆定理得到∠PMC=90°，于是得到结论；

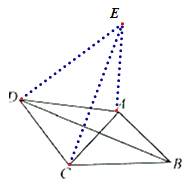
（3）根据已知可得△ABC是等腰直角三角形，所以将△ADB绕点A逆时针旋转90°，得到△ACE，则BD=CE，证明△DCE是直角三角形，再利用勾股定理可求CE值．

（1）∵，

∴，

在△ABD和△ACE中，

∵，

，

AD=AE，

∴△ABD≌△ACE，

∴；

（2）由小明的构造方法可得，

BP=BM=PM，∠PBM=∠PMB=60°，

∴∠ABP=∠CBM，

又∵AB=BC，

∴△BAP≌△BMC，

∴∠BPA=∠BMC，AP=CM，

∵，

∴，

设CM=3x，PM=4x，PC=5x，

∵(5x)2=(3x)2+(4x)2，

∴PC2=CM2+PM2，

∴△PCM是直角三角形，

∴∠PMC=90°，

∴∠BPA=∠BMC=60°+90°=150°；

（3）∵∠ACB=∠ABC=45°，

∴∠BAC=90°，且AC=AB．

将△ADB绕点A顺时针旋转90°，得到△ACE，

∴AD=AE，∠DAE=90°，BD=CE．

∴∠EDA=45°，DE=AD=4．

∵∠ADC=45°，

∴∠EDC=45°+45°=90°．

在Rt△DCE中，利用勾股定理可得，

CE= ，

∴BD=CE=．