题目内容
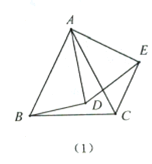
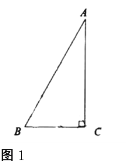
【题目】(1)在![]() 中,
中,![]() ,
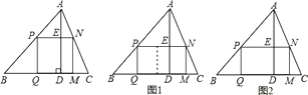
,![]() (如图1),
(如图1),![]() 与
与![]() 有怎样的数量关系?试证明你的结论.
有怎样的数量关系?试证明你的结论.
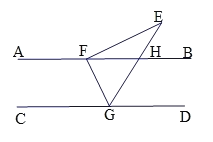
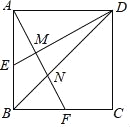
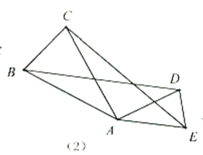
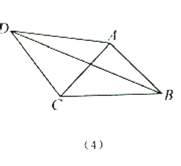
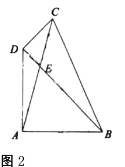
(2)图2,在四边形![]() 中,
中,![]() 相于点
相于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)AB=2BC,证明见解析;(2)![]() -1.
-1.
【解析】
(1)取AB的中点D,连接DC,得AD=BD=CD,再证明△DBC是等边三角形得BD=BC,从而可证明AB=2BC;
(2)过点A作AF⊥BD于点F,先确定∠2及∠3的度数,在Rt△AFB中求出AF,BF;Rt△AEF中,求出EF,AE,在Rt△ABD中求出DB,继而得出DE.
(1)AB=2BC
证明:取AB的中点D,连接DC,
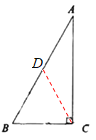
∵∠ACB=90°,CD为斜边AB上的中线
∴AD=BD=CD
∴∠A=∠ACD=30°,∠B=∠BCD
∴∠ADC=180°-∠A-∠ACD=120°
∴∠B=∠BCD=![]() ∠ADC=60°
∠ADC=60°
∴△DBC是等边三角形
∴BD=BC
∴AB=2BD=2BC
即AB=2BC
(2)过点A作AF⊥BD于点F,
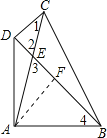
∵∠CDB=90°,∠1=30°,
∴∠2=∠3=60°,
在△AFB中,∠AFB=90°,
∵∠4=45°,AB=![]() ,
,
∴AF=BF=![]() ,
,
在Rt△AEF中,∠AFE=90°,
∴EF=1,AE=2,
在△ABD中,∠DAB=90°,AB=![]() ,
,
∴DB=2![]() ,
,
∴DE=DB-BF-EF=![]() -1.
-1.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】小明和他的同学根据抛掷两枚硬币时记录的实验结果,制作“出现两个正面”的频数、频率表如下:
抛掷次数 |
|
|
|
|
|
|
|
| |
出现两个正面的频数 |
|
|
|
|
|
|
|
| |
出现两个正面的频率 |
|
|
|
|
|
|
|
|
![]() 在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
![]() 小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢
小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢![]() 分;抛出其他结果–小明赢
分;抛出其他结果–小明赢![]() 分;谁先到
分;谁先到![]() 分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
分,谁就得胜.你认为这个游戏规则公平吗?说说理由.